题目内容
18.过点(2,$\sqrt{2}$)、($\sqrt{2}$,-$\sqrt{3}$)的椭圆的标准方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1.分析 设椭圆的方程为mx2+ny2=1,(m,n>0且m≠n),再由点(2,$\sqrt{2}$)、($\sqrt{2}$,-$\sqrt{3}$)代入椭圆方程,解方程即可得到m,n,进而得到所求标准方程.
解答 解:设椭圆的方程为mx2+ny2=1,(m,n>0且m≠n),
由题意可得$\left\{\begin{array}{l}{4m+2n=1}\\{2m+3n=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{1}{8}}\\{n=\frac{1}{4}}\end{array}\right.$,
即有椭圆方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1.
故答案为:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1.
点评 本题考查椭圆的标准方程的求法,注意运用待定系数法,考查运算求解能力,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
13.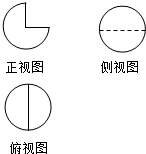 某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )
 某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )| A. | 14π | B. | 12π | C. | 10π | D. | 8π |
3.在等腰梯形ABCD中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x,其中x∈(0,1),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,若对任意x∈(0,1)都有不等式$t<\frac{{{{({e_1}+{e_2})}^2}}}{8}$恒成立,则t的最大值为( )
| A. | $\frac{7}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{5}{4}$ |
8.某几何体的三视图如图所示,则该几何体的体积为( )
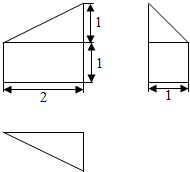

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{3}$ |
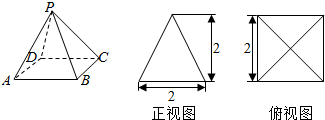 四棱锥P-ABCD及其正(主)视图和俯视图如图所示.
四棱锥P-ABCD及其正(主)视图和俯视图如图所示.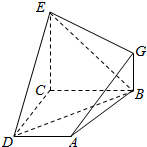 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD丄平面BCEG,BC=CD=CE=2AD=2BG=2.
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD丄平面BCEG,BC=CD=CE=2AD=2BG=2.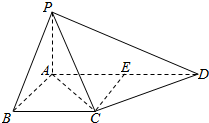 如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.