题目内容
19.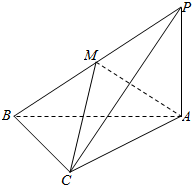 在三棱锥P-ABC中,∠PAB=∠PAC=∠ABC=90°,M是PB的中点,PA=AB=2.
在三棱锥P-ABC中,∠PAB=∠PAC=∠ABC=90°,M是PB的中点,PA=AB=2.(Ⅰ)求证:面PBC⊥面PAB;
(Ⅱ)若BC=1,求三棱锥A-PMC的体积.
分析 (1)由∠PAB=∠PAC=90°可知PA⊥平面ABC,故PA⊥BC,又由于BC⊥AB得出BC⊥平面PAB,所以面PBC⊥面PAB;
(2)由M为PB中点可得三棱锥A-PMC的体积为三棱锥P-ABC体积的一半.
解答 证明:(1)∵∠PAB=∠PAC=90°,∴PA⊥AB,PA⊥AC,
又∵AB?平面ABC,AC?平面ABC,AB∩AC=A,
∴PA⊥平面ABC,∵BC?平面ABC,
∴PA⊥BC,
∵∠ABC=90°,∴BC⊥AB,
又∵AB?平面PAB,PA?平面PAB,AB∩PA=A,
∴BC⊥平面PAB,∵BC?平面PBC,
∴面PBC⊥面PAB.
(2)∵M是PB的中点,
∴V棱锥M-ABC=$\frac{1}{2}$V棱锥P-ABC,
∴V棱锥A-PMC=V棱锥P-ABC-V棱锥M-ABC=$\frac{1}{2}$V棱锥P-ABC=$\frac{1}{2}×\frac{1}{3}$×$\frac{1}{2}$×1×2×2=$\frac{1}{3}$.
点评 本题考查了面面垂直的判定定理,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
8.某几何体的三视图如图所示,则该几何体的体积为( )
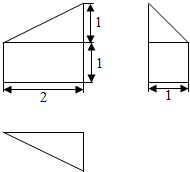

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{3}$ |
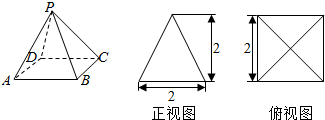 四棱锥P-ABCD及其正(主)视图和俯视图如图所示.
四棱锥P-ABCD及其正(主)视图和俯视图如图所示.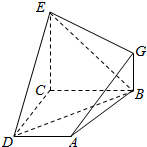 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD丄平面BCEG,BC=CD=CE=2AD=2BG=2.
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD丄平面BCEG,BC=CD=CE=2AD=2BG=2.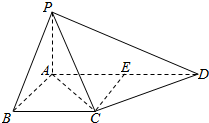 如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.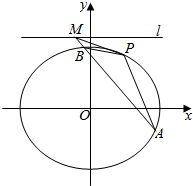 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,3),离心率e=$\frac{1}{2}$,直线1的方程为y=4.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,3),离心率e=$\frac{1}{2}$,直线1的方程为y=4.