题目内容
18.在△ABC中,角A,B,C的对边分别是a,b,c,且acosB-bcosA=$\frac{1}{2}$c.(Ⅰ)求证:tanA=3tanB;
(Ⅱ)若B=45°,b=$\sqrt{5}$,求△ABC的面积.
分析 (Ⅰ)题中等式利用正弦定理化简,利用同角三角函数间基本关系整理即可得证;
(Ⅱ)由tanB的值确定出tanA的值,进而求出sinA与cosA的值,由sinC=sin(A+B),利用两角和与差的正弦函数公式化简,将各自的值代入求出sinC的值,利用正弦定理求出c的值,由b,c,sinA的值,利用三角形面积公式即可求出三角形ABC面积.
解答 解:(Ⅰ)∵acosB-bcosA=$\frac{1}{2}$c,
∴由正弦定理化简得:sinAcosB-sinBcosA=$\frac{1}{2}$sinC=$\frac{1}{2}$sin(A+B)=$\frac{1}{2}$sinAcosB+$\frac{1}{2}$cosAsinB,
整理得:sinAcosB=3cosAsinB,
∵cosAcosB≠0,
∴tanA=3tanB;
(Ⅱ)∵tanA=3,∴sinA=$\frac{3}{\sqrt{10}}$,cosA=$\frac{1}{\sqrt{10}}$,
由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$得:a=$\frac{bsinA}{sinB}=3$
∵sinC=sin(A+B)=sinAcosB+cosAsinB=$\frac{3}{\sqrt{10}}×\frac{\sqrt{2}}{2}+\frac{1}{\sqrt{10}}×\frac{\sqrt{2}}{2}=\frac{2}{\sqrt{5}}$
∴∴S△ABC=$\frac{1}{2}$absinC$\frac{1}{2}$×3×$\sqrt{5}$×$\frac{2}{\sqrt{5}}$3.
点评 此题考查了正弦定理,同角三角函数间的基本关系,熟练掌握正弦定理是解本题的关键,属于中档题.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{10}$ | D. | $\frac{\sqrt{10}}{3}$ |
| A. | $-\frac{8}{9}$ | B. | $-\frac{1}{9}$ | C. | -8 | D. | 8 |
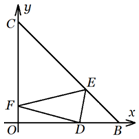 如图,△OBC为等腰直角三角形,∠BOC=90°,OB=3,BD=1,一束光线从点D入射,先后经过斜边BC与直角边OC反射后,恰好从点D射出,则该光线所走的路程是$\sqrt{26}$.
如图,△OBC为等腰直角三角形,∠BOC=90°,OB=3,BD=1,一束光线从点D入射,先后经过斜边BC与直角边OC反射后,恰好从点D射出,则该光线所走的路程是$\sqrt{26}$.