题目内容
若{an}是等比数列，其公比是q，且-a5，a4，a6成等差数列，则q等于（ ）
| A、1或2 |
| B、1或-2 |
| C、-1或 2 |
| D、-1或-2 |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：由题意可得-a5+a6=2a4 ，即-a4q+a4q2=2a4，化简可得（q+1）（q-2）=0，解方程求得q的值．
解答：
解：∵-a5，a4，a6成等差数列，
∴-a5+a6=2a4，
∴-a4q+a4q2=2a4，
∴q2-q-2=0，
∴（q+1）（q-2）=0，
∴q=-1或2．
故选：C．
∴-a5+a6=2a4，
∴-a4q+a4q2=2a4，
∴q2-q-2=0，
∴（q+1）（q-2）=0，
∴q=-1或2．
故选：C．
点评：本题主要考查等差数列的定义和性质，等比数列的定义和性质，等比数列的通项公式，得到（q+1）（q-2）=0，是解题的关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知m、n是两条不同的直线，α、β是两个不同的平面，给出下列命题：
①若α⊥β，m∥α，则m⊥β；
②若m⊥α，n⊥β，且m⊥n，则α⊥β；
③若m⊥β，m∥α，则α⊥β；
④若m∥α，n∥β，且m∥n，则α∥β．
其中正确命题的个数是（ ）
①若α⊥β，m∥α，则m⊥β；
②若m⊥α，n⊥β，且m⊥n，则α⊥β；
③若m⊥β，m∥α，则α⊥β；
④若m∥α，n∥β，且m∥n，则α∥β．
其中正确命题的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
f（x）是定义在R上的奇函数，且当x＞0时f（x）=ex-1，则当x＜0时（ ）
| A、f（x）=ex-1 |
| B、f（x）=e-x-1 |
| C、f（x）=-e-x+1 |
| D、f（x）=ex+1 |
已知数列{an}中，an=
，则S20=（ ）
| 1 |
| 4n2-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示的算法程序，则输出结果为（ ）
| A、2 | B、6 | C、42 | D、1806 |
圆x2+y2-4x+6y=0的圆心坐标，半径分别是（ ）
A、（-2，3），
| ||
B、（2，-3），
| ||
| C、（-2，-3），13 | ||
| D、（2，3），13 |
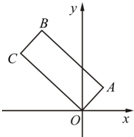如图，矩形OABC的顶点O为原点，AB边所在直线的方程为3x+4y-25=0，顶点B的纵坐标为10．
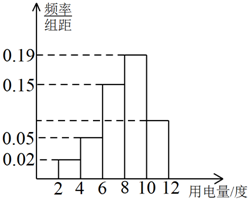为了解某地区用电高峰期居民的用电量，抽取一个容量为200的样本，记录某天各户居民的用电量（单位：度），制成频率分布直方图，如图．