题目内容
已知m、n是两条不同的直线,α、β是两个不同的平面,给出下列命题:
①若α⊥β,m∥α,则m⊥β;
②若m⊥α,n⊥β,且m⊥n,则α⊥β;
③若m⊥β,m∥α,则α⊥β;
④若m∥α,n∥β,且m∥n,则α∥β.
其中正确命题的个数是( )
①若α⊥β,m∥α,则m⊥β;
②若m⊥α,n⊥β,且m⊥n,则α⊥β;
③若m⊥β,m∥α,则α⊥β;
④若m∥α,n∥β,且m∥n,则α∥β.
其中正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:根据空间线面平行和垂直的几何特征及判定方法,逐一分析四个命题的真假,最后综合讨论结果,可得答案.
解答:
解:若α⊥β,m∥α,则m与β可能平行,可能相交,也可能线在面内,故①错误;
若m⊥α,且m⊥n,则n∥α或n?α,又由n⊥β,可得α⊥β,故②正确;
若m⊥β,m∥α,则存在直线a?α,使m∥a,则a⊥β,则α⊥β,故③正确;
若m∥α,n∥β,且m∥n,则α与β可能平行也可以相交,故④错误.
故正确命题的个数是2个,
故选:B
若m⊥α,且m⊥n,则n∥α或n?α,又由n⊥β,可得α⊥β,故②正确;
若m⊥β,m∥α,则存在直线a?α,使m∥a,则a⊥β,则α⊥β,故③正确;
若m∥α,n∥β,且m∥n,则α与β可能平行也可以相交,故④错误.
故正确命题的个数是2个,
故选:B
点评:本题以命题的真假判断为载体,考查了空间直线与平面的位置关系判定,熟练掌握空间线面关系的几何特征及判定方法是解答的关键.

练习册系列答案
相关题目
sin240°=( )
A、-
| ||||
| B、-1 | ||||
| C、-2 | ||||
| D、1 |
给出一个算法的程序框图(如图所示),该程序框图的功能是( )
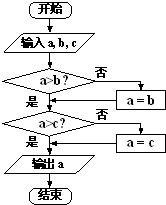

| A、求输出a,b,c三数的最大数 |
| B、求输出a,b,c三数的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
在等差数列{an}中,若a1+a3+a5=30,则a3=( )
| A、7 | B、8 | C、9 | D、10 |
已知在△ABC中,a=
,b=
,B=60°,那么角C等于( )
| 2 |
| 3 |
| A、135° | B、90° |
| C、45° | D、75° |
当a>0时,2a+
的最小值为( )
| 1 |
| a |
| A、3 | ||
B、2
| ||
| C、2 | ||
D、
|
下列方程中,t为参数.与方程y2=x表示同一曲线的是( )
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
若{an}是等比数列,其公比是q,且-a5,a4,a6成等差数列,则q等于( )
| A、1或2 |
| B、1或-2 |
| C、-1或 2 |
| D、-1或-2 |