题目内容
圆x2+y2-4x+6y=0的圆心坐标，半径分别是（ ）
A、（-2，3），
| ||
B、（2，-3），
| ||
| C、（-2，-3），13 | ||
| D、（2，3），13 |
考点：圆的一般方程
专题：直线与圆
分析：把圆的方程化为标准形式 （x-2）2+（y+3）2=13，求出圆心与半径，从而得到结论．
解答：
解：圆x2+y2-4x+6y=0，即（x-2）2+（y+3）2=13，表示以（2，-3）为圆心，以
为半径的圆，
故选：B．
| 13 |
故选：B．
点评：本题主要考查圆的标准方程的形式和特征，属于基础题．
练习册系列答案
相关题目
已知在△ABC中，a=
，b=
，B=60°，那么角C等于（ ）
| 2 |
| 3 |
| A、135° | B、90° |
| C、45° | D、75° |
为了得到函数y=sin3x+cos3x的图象，可以将函数y=
sin3x的图象（ ）
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
函数f（x）=x2+lnx的导数为（ ）
| A、f′（x）=2x+ex | ||
| B、f′（x）=2x+lnx | ||
C、f′（x）=2x+
| ||
D、f′（x）=2x-
|
若{an}是等比数列，其公比是q，且-a5，a4，a6成等差数列，则q等于（ ）
| A、1或2 |
| B、1或-2 |
| C、-1或 2 |
| D、-1或-2 |
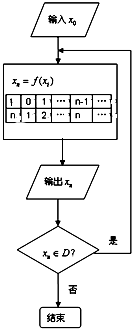对任意函数f（x），其定义域为D，可按如图所示，构造一个数列发生器，要求输入初始数据x0∈D，现定义f（x）=