题目内容
15.如图,在边长为2的正六边形ABCDEF中,则$\overrightarrow{AB}•\overrightarrow{AD}$=4.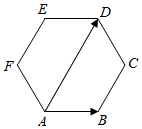
分析 根据正六边形的性质得出$\overrightarrow{AB},\overrightarrow{AD}$的模长和夹角,代入向量的数量积定义式计算.
解答 解:∵六边形ABCDEF是边长为2的正六边形,
∴AB=2,AD=4,∠BAD=60°,
∴$\overrightarrow{AB}•\overrightarrow{AD}$=4×2×cos60°=4.
故答案为:4.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
10.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)的图象与x轴的两个相邻交点之间的距离等于$\frac{π}{2}$,若将函数y=f(x)的图象向右平移$\frac{π}{12}$个单位长度得到函数y=g(x)的图象,则函数y=g(x)在区间[0,$\frac{π}{3}$]上的最大值为( )
| A. | 0 | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
7.设关于x、y的不等式组$\left\{\begin{array}{l}{2x-y+1>0}\\{3x-2<0}\\{y-a>0}\end{array}\right.$表示的平面区域内存在点P(x0,y0),满足x0-2y0=2,则a的取值范围是( )
| A. | (-∞,-$\frac{5}{3}$) | B. | (-∞,-$\frac{2}{3}$) | C. | (-∞,$\frac{1}{3}$) | D. | (-∞,$\frac{4}{3}$) |
4.已知不共线的两个向量$\overrightarrow a{,_{\;}}\overrightarrow b$满足$|{\overrightarrow a-\overrightarrow b}|=2$,且$\overrightarrow a⊥({\overrightarrow a-2\overrightarrow b})$,则$|{\overrightarrow b}|$=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
5.已知函数$y=2sin(2x+φ)(|φ|<\frac{π}{2})$的图象经过点(0,-1),则该函数的一个单调递增区间为( )
| A. | [-$\frac{π}{6}$,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{5π}{6}$] | C. | [-$\frac{5π}{12}$,$\frac{π}{12}$] | D. | [$\frac{π}{12}$,$\frac{7π}{12}$]] |
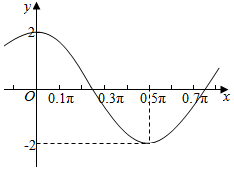 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.