题目内容

18．已知数列{an}中a1=1，an+1=an+2n（n∈N*）求其通项公式．

分析 当n≥2时，利用an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1，进而计算可得结论．

解答 解：当n≥2时，an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1
=2（n-1）+2（n-2）+…+2×1+1
=2×$\frac{n（n-1）}{2}$+1
=n2-n+1，
又∵a1=1满足上式，
∴an=n2-n+1．

点评 本题考查数列的通项公式，考查运算求解能力，注意解题方法的积累，属于基础题．

练习册系列答案
相关题目
8．已知数列{an}的前n项和为Sn，对任意n∈N*，Sn=（-1）nan+$\frac{1}{{2}^{n}}$+2n-6且（an+1-p）（an-p）＜0恒成立，则实数p的取值范围是$（{-\frac{7}{4}，\frac{23}{4}}）$．
9．在△ABC中，角A，B，C所对的边分别为a，b，c．若$bcosC+\frac{csinB}{{\sqrt{3}}}=a$．
（1）求角B的大小；
（2）若△ABC的面积为$\sqrt{3}$，A＞C，且其外接圆的面积为4π．试求边a与边c的值．
6．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，右焦点F2到直线x+y+5=0的距离为3$\sqrt{2}$．
（1）求椭圆C的方程；
（2）若直线l经过椭圆C的右焦点F2，且与抛物线y2=4x交于A1，A2两点，与椭圆C交于B1，B2两点，当以B1B2为直径的圆经过椭圆C的左焦点F1时，求以A1A2为直径的圆的标准方程．
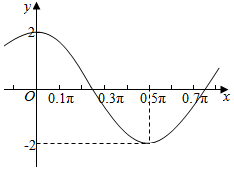13．已知函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的图象如图所示．
（1）求A，ω，φ的值；
（2）若y=1，求对应x的值．
3．已知函数f（x）=xlnx+a，直线y=x与曲线y=f（x）相切．
（Ⅰ）求a的值；
（Ⅱ）证明：xex-1[f（x）-2]+f（x）≥0．
10．若α∈（π，$\frac{3}{2}$π），tanα=$\frac{5}{12}$，求tan$\frac{α}{2}$．
7．函数y=（x-1）2（x≥1）的反函数y=1+$\sqrt{x}$（x≥0）．
20．（x2+x+1）（1-x）4展开式中x2的系数为3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网