题目内容
4.已知圆心为C的圆经过点A(0,2)和B(1,1),且圆心C在直线l:x+y+5=0上.(1)求圆C的标准方程;
(2)若P(x,y)是圆C上的动点,求3x-4y的最大值与最小值.
分析 (1)根据条件求出圆心和半径即可求出圆的标准方程.
(2)根据直线和圆的位置关系进行求解即可.
解答 解:(1)线段AB的中点为$(\frac{1}{2},\frac{3}{2})$,又kAB=-1
故线段AB的垂直平分线方程为$y-\frac{3}{2}=1•(x-\frac{1}{2})$即x-y+1=0…(2分)
由$\left\{\begin{array}{l}x-y+1=0\\ x+y+5=0\end{array}\right.$得圆心C(-3,-2)…(4分)
圆C的半径长$r=|AC|=\sqrt{{{(0+3)}^2}+{{(2+2)}^2}}=5$
故圆C的标准方程为(x+3)2+(y+2)2=25…(6分)
(2)令z=3x-4y,即3x-4y-z=0
当直线3x-4y-z=0与圆C相切于点P时,z取得最值…(8分)
则圆心C(-3,-2)到直线3x-4y-z=0的距离为$d=\frac{|-9+8-z|}{{\sqrt{{3^2}+{{(-4)}^2}}}}=5$,解得z=-26或z=24
故3x-4y的最小值为-26,最大值为24…(12分)
点评 本题主要考查圆的标准方程的求解,利用直线和圆的位置关系是解决本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.如图所示的程序框图输出的结果是( )
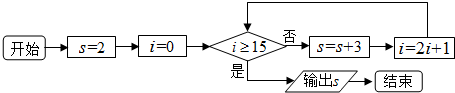

| A. | s=31 | B. | s=17 | C. | s=11 | D. | s=14 |
19.已知点M(a,b)在圆O:x2+y2=4外,则直线ax+by=4与圆O的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不确定 |
9.若l,m,n是不相同的空间直线,α,β是不重合的两个平面,则下列命题正确的是( )
| A. | l⊥α,m⊥β,l⊥m⇒α⊥β | B. | l∥m,m⊆α⇒l∥α | ||
| C. | l⊆α,m⊆α,l∥β,m∥β⇒α∥β | D. | l⊥n,m⊥n⇒l∥m |
13.已知命题p:?x∈R,|x|<0,则¬p是( )
| A. | ?x∈R,|x|≥0 | B. | ?x∈R,|x|>0 | C. | ?x∈R,|x|≥0 | D. | ?x∈R,|x|<0 |
14.如果a>b>0,那么下列不等式成立的是( )
| A. | a2>ab | B. | ab<b2 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | $\frac{b}{a}$>$\frac{a}{b}$ |
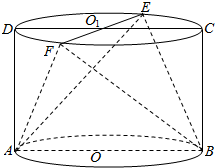 在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),AB=2,BC=$\sqrt{2}$.
在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),AB=2,BC=$\sqrt{2}$.