题目内容
9.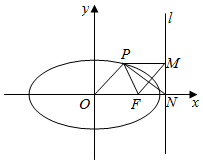 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点为F,右准线l交x轴于点N,过椭圆上一点P作PM垂直于准线l,垂足为M,若PN平分∠FPM,且四边形OFMP为平行四边形.证明:e$>\frac{2}{3}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点为F,右准线l交x轴于点N,过椭圆上一点P作PM垂直于准线l,垂足为M,若PN平分∠FPM,且四边形OFMP为平行四边形.证明:e$>\frac{2}{3}$.
分析 利用四边形OFMP为平行四边形,可设点P坐标,进而可求出直线PF的方程不等式,通过PN平分∠FPM,利用角平分线的性质,化简可知e6-e4+2e2-1=0,通过令f(x)=x6-x4+2x2-1,求导可知f(x)在(0,1)上单调递增,利用f($\frac{2}{3}$)<0、f(1)>0即得结论.
解答 证明:依题意,可知F(c,0),N($\frac{{a}^{2}}{c}$,0),
∵四边形OFMP为平行四边形,
∴P($\frac{{a}^{2}}{c}$-c,$\frac{b}{ac}$$\sqrt{{a}^{2}{c}^{2}-{b}^{4}}$),
∴直线PF的方程为:$\frac{y-0}{x-c}$=$\frac{\frac{b}{ac}\sqrt{{a}^{2}{c}^{2}-{b}^{4}}}{\frac{{a}^{2}}{c}-c-c}$,
整理得:b$\sqrt{{a}^{2}{c}^{2}-{b}^{4}}$x-a(a2-2c2)y-bc$\sqrt{{a}^{2}{c}^{2}-{b}^{4}}$=0,
∵PN平分∠FPM,
∴$\frac{b}{ac}$$\sqrt{{a}^{2}{c}^{2}-{b}^{4}}$=$\frac{|b\sqrt{{a}^{2}{c}^{2}-{b}^{4}}•\frac{{a}^{2}}{c}-0-bc\sqrt{{a}^{2}{c}^{2}-{b}^{4}}|}{\sqrt{{b}^{2}({a}^{2}{c}^{2}-{b}^{4})+{a}^{2}({a}^{2}-2{c}^{2})^{2}}}$,
整理得:a6-b6-3a4b2+2a2b4=0,
两边同时除以a6,得:1-$\frac{{b}^{6}}{{a}^{6}}$-3$\frac{{b}^{2}}{{a}^{2}}$+2$\frac{{b}^{4}}{{a}^{4}}$=0,
又∵$\frac{{b}^{2}}{{a}^{2}}$=1-e2,
∴1-(1-e2)3-3(1-e2)+2(1-e2)2=0,
整理得:e6-e4+2e2-1=0,
记f(x)=x6-x4+2x2-1,则f′(x)=6x5-4x3+4x=6x[(x2-1)2+$\frac{5}{9}$],
显然当0<x<1时,f′(x)>0,即函数在(0,1)上单调递增,
又∵f($\frac{2}{3}$)=$(\frac{2}{3})^{6}$-$(\frac{2}{3})^{4}$+2$(\frac{2}{3})^{2}$-1=-$\frac{161}{729}$<0,
f(1)=1-1+2-1=1>0,
∴当$\frac{2}{3}$<x<1时,方程f(x)=0才有唯一解,
故e$>\frac{2}{3}$.
点评 本题考查椭圆的简单性质,考查运算求解能力,考查利用导数研究函数的单调性,注意解题方法的积累,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1070人 | B. | 1030人 | C. | 930人 | D. | 970人 |
| A. | 一个三棱柱可以由一个三棱锥和一个四棱锥拼合而成 | |
| B. | 一个圆台可以由两个圆台拼合而成 | |
| C. | 一个圆锥可以由两个圆锥拼合而成 | |
| D. | 一个四棱台可以由两个四棱台拼合而成 |
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{9}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{2\sqrt{3}}{9}$ |
| A. | 5039 | B. | 5040 | C. | 5041 | D. | 5042 |