题目内容
19.函数f(x)=1+$\frac{sinx}{2+cosx}$的最大值与最小值之和为2.分析 把已知等式变形,利用辅助角公式化积,然后利用三角函数的有界性转化为关于y的不等式求解.
解答 解:由y=f(x)=1+$\frac{sinx}{2+cosx}$,得sinx-(y-1)cosx=2(y-1),
∴$\sqrt{1+(y-1)^{2}}(\frac{1}{\sqrt{1+(y-1)^{2}}}sinx-\frac{y-1}{\sqrt{1+(y-1)^{2}}}cosx)=2(y-1)$,
即sin(x-θ)=$\frac{2(y-1)}{\sqrt{1+(y-1)^{2}}}$(tanθ=y-1),
由|$\frac{2(y-1)}{\sqrt{1+(y-1)^{2}}}$|≤1,得3y2-6y+2≤0,解得:$\frac{3-\sqrt{3}}{3}≤y≤\frac{3+\sqrt{3}}{3}$.
∴函数f(x)=1+$\frac{sinx}{2+cosx}$的最大值与最小值分别为$\frac{3+\sqrt{3}}{3},\frac{3-\sqrt{3}}{3}$,和为2.
故答案为:2.
点评 本题考查三角函数的最值的求法,训练了利用三角函数的有界性求函数的最值,是中档题.

练习册系列答案
相关题目
7.袋中装有6个红球和4个白球,不放回地一次摸出一个,在第一次摸出红球的条件下,第二次摸到红球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{5}{9}$ |
2.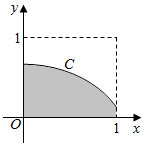 在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
附:若X~N(μ,σ2),则P(μ-δ<X≤μ+δ)=0.6826,P(μ-2δ<X≤μ+2δ)=0.9544.
 在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )附:若X~N(μ,σ2),则P(μ-δ<X≤μ+δ)=0.6826,P(μ-2δ<X≤μ+2δ)=0.9544.
| A. | 3413 | B. | 1193 | C. | 2718 | D. | 6587 |
3. 如图,正方形ABCD中,M、N分别是BC、CD的中点,若$\overrightarrow{AC}$=λ$\overrightarrow{AM}$+μ$\overrightarrow{BN}$,则λ+μ=( )
如图,正方形ABCD中,M、N分别是BC、CD的中点,若$\overrightarrow{AC}$=λ$\overrightarrow{AM}$+μ$\overrightarrow{BN}$,则λ+μ=( )
 如图,正方形ABCD中,M、N分别是BC、CD的中点,若$\overrightarrow{AC}$=λ$\overrightarrow{AM}$+μ$\overrightarrow{BN}$,则λ+μ=( )
如图,正方形ABCD中,M、N分别是BC、CD的中点,若$\overrightarrow{AC}$=λ$\overrightarrow{AM}$+μ$\overrightarrow{BN}$,则λ+μ=( )| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{6}{5}$ | D. | $\frac{8}{5}$ |
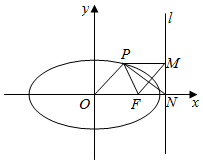 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点为F,右准线l交x轴于点N,过椭圆上一点P作PM垂直于准线l,垂足为M,若PN平分∠FPM,且四边形OFMP为平行四边形.证明:e$>\frac{2}{3}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点为F,右准线l交x轴于点N,过椭圆上一点P作PM垂直于准线l,垂足为M,若PN平分∠FPM,且四边形OFMP为平行四边形.证明:e$>\frac{2}{3}$.