题目内容
18.已知函数y=f(x)满足f(2x)=2f(x),当1≤x≤2时,f(x)=$\frac{1}{2}$-|x-$\frac{3}{2}$|,当x∈[1,2n],n∈N*时,函数y=f(x)的图象与x轴所围成的图形面积记为Sn,则S1=$\frac{1}{4}$,Sn=$\frac{1}{12}$(4n-1).分析 结合函数的性质作函数y=f(x)的部分图象,将[1,2n]分割成[1,2],[2,4],[4,8],[8,16],…,[2n-1,2n]个部分,从而可得各部分的面积,从而求和即可.
解答 解:∵f(2x)=2f(x),当1≤x≤2时,f(x)=$\frac{1}{2}$-|x-$\frac{3}{2}$|,
∴作函数y=f(x)的部分图象如下图,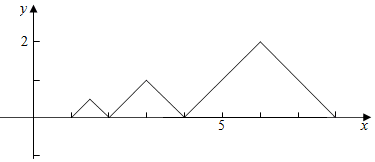 ,
,
将[1,2n]分割成[1,2],[2,4],[4,8],[8,16],…,[2n-1,2n]个部分,
设在各区间内的面积依次为a1,a2,a3,…,an;
则结合图象可得,a1=$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$,an=4an-1,
故S1=a1=$\frac{1}{4}$,Sn=$\frac{\frac{1}{4}(1-{4}^{n})}{1-4}$=$\frac{1}{12}$(4n-1),
故答案为:$\frac{1}{4}$,$\frac{1}{12}$(4n-1).
点评 本题考查了分段函数与绝对值函数的应用及转化思想与分类讨论及数形结合的思想应用,同时考查了数列的应用,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
8.已知集合A={y|y=2x-1,x∈R},B={x|x-x2>0},则A∩B=( )
| A. | (-1,+∞) | B. | (-1,1) | C. | (-1,0) | D. | (0,1) |
13.在△ABC中,tanA+tanC=3tanB,则tanB的取值范围是( )
| A. | (0,+∞) | B. | [1,+∞) | C. | [$\frac{4}{3}$,+∞) | D. | [1,$\frac{4}{3}$] |
7.袋中装有6个红球和4个白球,不放回地一次摸出一个,在第一次摸出红球的条件下,第二次摸到红球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{5}{9}$ |
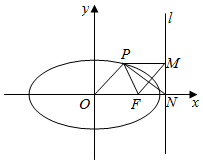 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点为F,右准线l交x轴于点N,过椭圆上一点P作PM垂直于准线l,垂足为M,若PN平分∠FPM,且四边形OFMP为平行四边形.证明:e$>\frac{2}{3}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点为F,右准线l交x轴于点N,过椭圆上一点P作PM垂直于准线l,垂足为M,若PN平分∠FPM,且四边形OFMP为平行四边形.证明:e$>\frac{2}{3}$.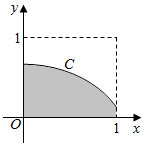 在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )