题目内容
“α为锐角”是“sinα＞0”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据三角函数的性质，利用充分条件和必要条件的定义进行判断即可得到结论．
解答：
解：若“α为锐角”则“sinα＞0”成立，即充分性成立，
当α=90°时，满足sinα=1＞0，但α为锐角不成立，即必要性不成立，
故“α为锐角”是“sinα＞0”的充分不必要条件，
故选：A
当α=90°时，满足sinα=1＞0，但α为锐角不成立，即必要性不成立，
故“α为锐角”是“sinα＞0”的充分不必要条件，
故选：A
点评：本题主要考查充分条件和必要条件的判断，根据三角函数的性质是解决本题的关键．
练习册系列答案
智能训练练测考系列答案
相关题目
设有穷数列{an}（n=1，2，…，n），Sn是其前n项和，定义
为{an}的“凯森和”．今有500项的数列a1，a2，…，a500的“凯森和”为2004，则有501项的数列2，a1，a2，…，a500的“凯森和”为（ ）
| S1+S2+…+Sn |
| n |
| A、2002 | B、2004 |
| C、2008 | D、2014 |
已知函数f（x）=|
-1|，若存在正实数a，b（a＜b），使得集合{y|y=f（x），a≤x≤b}=[ma，mb]，则m的取值范围为（ ）
| 1 |
| x |
A、（0，
| ||||
B、（0，
| ||||
C、（
| ||||
D、（
|
若函数f（x）在给定区间M上存在正数t，使得对于任意的x∈M，有x+t∈M，且f（x+t）≥f（x），则称f（x）为M上t级类增函数，则下列命题中正确的是（ ）
A、函数f（x）=
| ||||||
| B、函数f（x）=|log2（x-1）|是（1，+∞）上的1级类增函数 | ||||||
C、若函数f（x）=sinx+ax为[
| ||||||
| D、若函数f（x）=x2-3x为[1，+∞）上的t级类增函数，则实数t的取值范围为[2，+∞） |
在△ABC中，若B=120°，AC=
，则
=（ ）
| 3 |
| BC |
| sinA |
| A、2 | ||||
| B、1 | ||||
C、
| ||||
D、
|
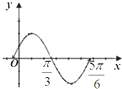
已知函数y=2sin（ωx+φ）（ω＞0，|φ|＜
）的图象的一部分如图所示，则（ ）
| π |
| 2 |
A、ω=2，φ=
| ||
B、ω=2，φ=-
| ||
C、ω=2，φ=
| ||
D、ω=2，φ=-
|
已知直线的倾斜角的余弦值是
，则此直线的斜率是（ ）
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、±
|