题目内容
13.设R为实数集,集合S={x|log2x>0},T={x|x2>4},则S∩(∁RT)=( )| A. | {x|1<x<2} | B. | {x|1≤x<2} | C. | {x|1<x≤2} | D. | {x|1≤x≤2} |
分析 解对数不等式求得S、解一元二次不等式求得T,再根据补集的定义求得∁RT,从而求得S∩(∁RT).
解答 解:∵log2x>0=log21,
∴x>1,
∴S={x|x>1},
∵x2>4,
∴|x|>2,
∴x>2或x<2,
∴T={x|x>2或x<2},
∴∁RT={x|-2≤x≤2],
∴S∩(∁RT)={x|1<x≤2}.
故选:C.
点评 本题考查了交、并、补集的混合运算,熟练掌握交、并、补集的定义是解本题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
3.已知三个平面两两垂直,给出命题:①它们的交线一定交于一点; ②它们的交线一定两两垂直; ③其中任意两个平面的交线一定与第三个平面垂直;④它们将空间分成8部分; 其中正确的命题一共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.函数f(x)=cosx,x∈[0,2π]与直线y=1所围区域的面积为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
1.已知实数x,y满足$\left\{\begin{array}{l}{x-y+3≥0}\\{x+y-1≥0}\\{x≤1}\end{array}\right.$,若直线x+ky-1=0将可行域分成面积相等的两部分,则实数k的值为( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
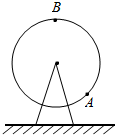 乐场有一个按逆时针方向旋转的大风车,如图所示.已知某人从点A处上风车,离地面的高度h(米)与它登上大风车后运行的时间t(分钟)满足函数关系h=12.5+10cos($\frac{2π}{15}$t-$\frac{2π}{3}$),且5分钟后到达顶点B.
乐场有一个按逆时针方向旋转的大风车,如图所示.已知某人从点A处上风车,离地面的高度h(米)与它登上大风车后运行的时间t(分钟)满足函数关系h=12.5+10cos($\frac{2π}{15}$t-$\frac{2π}{3}$),且5分钟后到达顶点B.