题目内容
1.已知实数x,y满足$\left\{\begin{array}{l}{x-y+3≥0}\\{x+y-1≥0}\\{x≤1}\end{array}\right.$,若直线x+ky-1=0将可行域分成面积相等的两部分,则实数k的值为( )| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
分析 作出不等式组对应的平面区域,根据直线将平面区域分成面积相等的两部分,得到直线过AB的中点,求出相应的坐标即可得到k的值.
解答  解:作出不等式组对应平面区如图(三角形ABC部分):
解:作出不等式组对应平面区如图(三角形ABC部分):
∵直线x+ky-1=0过定点C(1,0),
∴C点也在平面区域ABC内,
要使直线x+ky-1=0将可行域分成面积相等的两部分,
则直线x+ky-1=0必过线段AB的中点D.
由$\left\{\begin{array}{l}{x=1}\\{x-y+3=0}\end{array}\right.$,解得B(1,4),
由$\left\{\begin{array}{l}{x-y+3=0}\\{x+y-1=0}\end{array}\right.$,解得A(-1,2),
∴AB的中点DD(0,3),
将D的坐标代入直线x+ky-1=0得3k-1=0,
解得k=$\frac{1}{3}$,
故选:C.
点评 本题主要考查二元一次不等式组表示平面区域以及三角形的面积的应用,利用数形结合是解决本题的关键,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.“m<5”是“|m|<5”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.已知数列{an}中,an>0,a1=1,${a_{n+2}}=\frac{1}{{{a_n}+1}}$,a100=a96,则a2016+a3=( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{1+\sqrt{5}}}{2}$ | C. | $\frac{{-1+\sqrt{5}}}{2}$ | D. | $\frac{5}{2}$ |
13.设R为实数集,集合S={x|log2x>0},T={x|x2>4},则S∩(∁RT)=( )
| A. | {x|1<x<2} | B. | {x|1≤x<2} | C. | {x|1<x≤2} | D. | {x|1≤x≤2} |
10.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
(1)若某人一月份应缴纳此项税款为280元,那么他当月的工资、薪金所得是多少?
(2)假设某人一个月的工资、薪金所得是x元(0<x≤10000),试将其当月应缴纳此项税款y元表示成关于x的函数.
| 全月应纳税所得额 | 税率(%) |
| 不超过1500元的部分 | 3 |
| 超过1500元至4500元的部分 | 10 |
| 超过4500元至9000元的部分 | 20 |
(2)假设某人一个月的工资、薪金所得是x元(0<x≤10000),试将其当月应缴纳此项税款y元表示成关于x的函数.
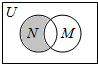 设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.