题目内容
5.质检过后,某校为了解理科班学生的数学、物理学习情况,利用随机数表法从全年级600名理科生抽取100名学生的成绩进行统计分析,已知学生考号的后三位分别为000,001,002,…,599.(1)若从随机数表的第5行第7列的数开始向右读,请依次写出抽取的前7人的后三位考号;
(2)如果题(1)中随机抽取到的7名同学的数学、物理成绩(单位:分)对应如表:
| 数学成绩 | 90 | 97 | 105 | 113 | 127 | 130 | 135 |
| 物理成绩 | 105 | 116 | 120 | 127 | 135 | 130 | 140 |

分析 (1)从随机数表的第5行第7列的数开始向右读,依次写出抽取的前7人的后三位考号为:310,503,315,571,210,142,188.
(2)这7名同学中数学和物理成绩均为优秀的人数为3人,因此ζ取值为0,1,2,3.ξ~B$(3,\frac{3}{7})$.根据P(ξ=k)=${∁}_{3}^{k}(\frac{4}{7})^{3-k}(\frac{3}{7})^{k}$,即可得出.
解答 解:(1)从随机数表的第5行第7列的数开始向右读,依次写出抽取的前7人的后三位考号为:310,503,315,571,210,142,188.
(2)这7名同学中数学和物理成绩均为优秀的人数为3人,因此ζ取值为0,1,2,3.
ξ~B$(3,\frac{3}{7})$.
∴P(ξ=k)=${∁}_{3}^{k}(\frac{4}{7})^{3-k}(\frac{3}{7})^{k}$,
可得P(ξ=0)=$\frac{64}{343}$,P(ξ=1)=$\frac{144}{343}$,P(ξ=2)=$\frac{108}{343}$,P(ξ=3)=$\frac{27}{343}$.
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{64}{343}$ | $\frac{144}{343}$ | $\frac{108}{343}$ | $\frac{27}{343}$ |
点评 本题考查了二项分布列的概率计算及其数学期望、随机数表的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
15.在直三棱柱ABC-A1B1C1中,AB=BC=1,AC=$\sqrt{2}$,BB1=2,点M为BB1的中点,则点A到平面A1CM距离为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
16.若复数$z=\frac{1+i}{1-i}$,$\overline z$为z的共轭复数,则${({\overline z})^{2017}}$=( )
| A. | i | B. | -i | C. | -22017i | D. | 22017i |
20.在△ABC中,内角A,B,C所对的边分别为a,b,c,且BC边上的高为$\frac{a}{2}$,则$\frac{c}{b}+\frac{b}{c}$最大值为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |
10.在平面直角坐标系中,矩形ABCD的对角线所在的直线相较于(0,1),若边AB所在的直线的方程为x-2y-2=0,则圆(x-1)2+(y-1)2=9被直线CD所截的弦长为( )
| A. | 3 | B. | $2\sqrt{3}$ | C. | 4 | D. | $3\sqrt{2}$ |
17.已知M是面积为1的△ABC内的一点(不含边界),若△MBC,△MCA和△MAB的面积分别为x,y,z,则$\frac{1}{x+y}$+$\frac{x+y}{z}$的最小值是( )
| A. | 2 | B. | 3 | C. | 3.5 | D. | 4 |
15.设一圆锥的外接球与内切球的球心位置相同,且外接球的半径为2,则该圆锥的体积为( )
| A. | π | B. | 3π | C. | 8π | D. | 9π |
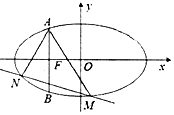 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F为抛物线y2=-4x的焦点,过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F为抛物线y2=-4x的焦点,过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.