题目内容
20.在△ABC中,内角A,B,C所对的边分别为a,b,c,且BC边上的高为$\frac{a}{2}$,则$\frac{c}{b}+\frac{b}{c}$最大值为( )| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |
分析 由已知可得:$\frac{1}{2}$a×$\frac{a}{2}$=$\frac{1}{2}bcsinA$,可得2bcsinA=a2=b2+c2-2bccosA,$\frac{b}{c}+\frac{c}{b}$=2sinA+2cosA=2$\sqrt{2}$sin$(A+\frac{π}{4})$,即可得出.
解答 解:由已知可得:$\frac{1}{2}$a×$\frac{a}{2}$=$\frac{1}{2}bcsinA$,可得2bcsinA=a2=b2+c2-2bccosA,
∴$\frac{b}{c}+\frac{c}{b}$=2sinA+2cosA=2$\sqrt{2}$sin$(A+\frac{π}{4})$≤2$\sqrt{2}$,当且仅当A=$\frac{π}{4}$时取等号.
故选:C.
点评 本题考查了三角形面积计算公式、余弦定理、三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知$\overrightarrow{a}$=(-2,1),$\overrightarrow{b}$=(k,-3),$\overrightarrow{c}$=(1,2),若($\overrightarrow{a}$-2$\overrightarrow{b}$)⊥$\overrightarrow{c}$,则|$\overrightarrow{b}$|=( )
| A. | $3\sqrt{5}$ | B. | 3$\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{10}$ |
5.质检过后,某校为了解理科班学生的数学、物理学习情况,利用随机数表法从全年级600名理科生抽取100名学生的成绩进行统计分析,已知学生考号的后三位分别为000,001,002,…,599.
(1)若从随机数表的第5行第7列的数开始向右读,请依次写出抽取的前7人的后三位考号;
(2)如果题(1)中随机抽取到的7名同学的数学、物理成绩(单位:分)对应如表:
从这7名同学中随机抽取3名同学,记这3名同学中数学和物理成绩均为优秀的人数为ζ,求ζ的分布列和数学期望(规定成绩不低于120分的为优秀).附:(下面是摘自随机数表的第4行到第6行)

(1)若从随机数表的第5行第7列的数开始向右读,请依次写出抽取的前7人的后三位考号;
(2)如果题(1)中随机抽取到的7名同学的数学、物理成绩(单位:分)对应如表:
| 数学成绩 | 90 | 97 | 105 | 113 | 127 | 130 | 135 |
| 物理成绩 | 105 | 116 | 120 | 127 | 135 | 130 | 140 |

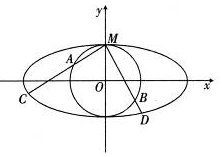 如图,圆O(O为坐标原点)与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于点M(0,1).
如图,圆O(O为坐标原点)与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于点M(0,1).