题目内容
函数y=
(sinx+cosx)的单调递增区间是 .
| 1 |
| 2 |
考点:两角和与差的正弦函数
专题:三角函数的图像与性质
分析:利用两角和差的正弦公式和正弦函数的单调性即可得出.
解答:
解:∵函数y=
(sinx+cosx)=
(
simx+
cosx)=
(sinxcos
+cosxsin
)=
sin(x+
).
由-
+2kπ≤x+
≤
+2kπ(k∈Z),
解得-
+2kπ≤x≤
+2kπ(k∈Z).
∴函数y=
(sinx+cosx)的单调递增区间是[-
+2kπ,
+2kπ](k∈Z).
故答案为:[-
+2kπ,
+2kπ](k∈Z).
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
由-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得-
| 3π |
| 4 |
| π |
| 4 |
∴函数y=
| 1 |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
故答案为:[-
| 3π |
| 4 |
| π |
| 4 |
点评:本题考查了两角和差的正弦公式和正弦函数的单调性,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
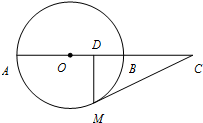 如图,AB为圆O的直径,AB=2,过圆O上一点M作圆O的切线,交AB的延长线于点C,过点M作MD⊥AB于点D,若D是OB中点.则AC•BC=
如图,AB为圆O的直径,AB=2,过圆O上一点M作圆O的切线,交AB的延长线于点C,过点M作MD⊥AB于点D,若D是OB中点.则AC•BC= 如图,抛物线y=-x2+2(m+1)x+m+3与x轴交于A、B两点,且OA:OB=3:1,则m=
如图,抛物线y=-x2+2(m+1)x+m+3与x轴交于A、B两点,且OA:OB=3:1,则m=