题目内容
4.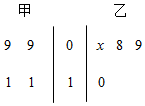 从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.
从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.(1)求X,若儿童身高B(cm)与年龄A(岁)的关系是B=7A+70,试分别估计甲、乙两个班级同学的平均身高;
(2)由茎叶图直接估计哪一个班学生的身高更整齐,说明理由.
分析 (1)根据平均数的定义求出X的值,再求甲、乙两班的平均年龄和平均身高;
(2)由茎叶图中的数据,结合方差的意义,即可得出结论.
解答 解:(1)根据茎叶图中的数据,得
这8个同学的平均年龄是$\frac{1}{8}$×(9+9+11+11+X+8+9+10)=9.5,
解得X=9;
甲班同学的平均年龄为$\overline{{x}_{甲}}$=$\frac{1}{4}$×(9+9+11+11)=10(岁),
平均身高为B甲=7×10+70=140(cm);
乙班同学的平均年龄为$\overline{{x}_{乙}}$=$\frac{1}{4}$×(9+8+9+10)=9(岁)
平均身高为B乙=7×9+70=133(cm);
(2)由茎叶图中的数据知,
甲班学生的年龄在9~11之间,较为分散些,所以身高较为分散些;
乙班学生的年龄在8~10之间,较为集中些,所以身高较为集中些;
即估计乙班学生的身高更整齐.
点评 本题考查了茎叶图的应用问题,也考查了平均数与方差的应用问题,是基础题目.

练习册系列答案
相关题目
16.在等比数列{an}中,an>0(n∈N+),公比q∈(0,1)且a2a4+2a3a5+a1a9=25,又a3与a5的等比中项为2,bn=log2an,数列{bn}的前n项和为Sn,则当{$\frac{{S}_{n}}{n}$}的前n项和Tn最大时,n的值为( )
| A. | 8 | B. | 9 | C. | 8或9 | D. | 17 |
16.已知抛物线y2=20x的焦点到双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线的距离为4,则该双曲线的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
13.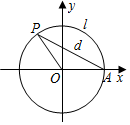 如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
 如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π| A. | 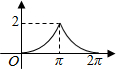 | B. | 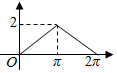 | C. |  | D. |  |
14.若正实数m、n满足3m+4n=5mn,则m+3n的最小值是( )
| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{28}{5}$ |