题目内容
16.在等比数列{an}中,an>0(n∈N+),公比q∈(0,1)且a2a4+2a3a5+a1a9=25,又a3与a5的等比中项为2,bn=log2an,数列{bn}的前n项和为Sn,则当{$\frac{{S}_{n}}{n}$}的前n项和Tn最大时,n的值为( )| A. | 8 | B. | 9 | C. | 8或9 | D. | 17 |
分析 利用等差数列与等比数列的通项公式及其前n项和公式即可得出.
解答 解:a3与a5的等比中项为2,∴a3•a5=22=4,
又an>0(n∈N+),公比q∈(0,1)且a2a4+2a3a5+a1a9=25,
∴$\frac{4}{{q}^{2}}$+2×4+4q2=25,
化为4q4-17q2+4=0,
解得q2=$\frac{1}{4}$,4(舍去).
联立解得:a1=16,q=$\frac{1}{2}$.
∴an=$16×(\frac{1}{2})^{n-1}$=25-n.
bn=log2an=5-n.
数列{bn}的前n项和为Sn=$\frac{n(4+5-n)}{2}$=$\frac{n(9-n)}{2}$.
∴$\frac{{S}_{n}}{n}$=$-\frac{1}{2}n$+$\frac{9}{2}$.
令$-\frac{1}{2}n$+$\frac{9}{2}$≥0,解得n≤9.
则当{$\frac{{S}_{n}}{n}$}的前n项和Tn最大时,n的值为8,或9.
故选:C.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
6.若直线y=ax是曲线y=2lnx+1的一条切线,则实数a=( )
| A. | e-${\;}^{\frac{1}{2}}$ | B. | 2e-${\;}^{\frac{1}{2}}$ | C. | e${\;}^{\frac{1}{2}}$ | D. | 2e${\;}^{\frac{1}{2}}$ |
11.若关于x的方程x2+2kx-1=0的两根x1,x2满足-1≤x1<0<x2<2,则k的取值范围是( )
| A. | (-$\frac{3}{4}$,0) | B. | (-$\frac{3}{4}$,0] | C. | (0,$\frac{3}{4}$) | D. | [0,$\frac{3}{4}$) |
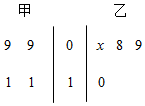 从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.
从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.