题目内容
9.有下列四个说法:①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
②“命题p∨q为真”是“命题p∧q为真”的必要不充分条件;
③命题“已知x,y∈R,若x<1或y<2,则x+y<3”的逆命题为真命题;
④在区间[0,π]上随机取一个数x,则事件“$tanx•cosx≥\frac{1}{2}$”发生的概率为$\frac{5}{6}$;
其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据特称命题的否定是全称命题进行判断,
②根据复合命题与充分条件和必要条件的定义进行判断,
③根据四种命题之间的关系进行判断,
④根据几何概型的概率公式进行判断.
解答 解:①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”正确,故①正确;
②当p真q假时,满足命题p∨q为真但命题p∧q为假,即充分性不成立,
若p∧q为真,则p,q同时为真,则p∨q为真,即②“命题p∨q为真”是“命题p∧q为真”的必要不充分条件正确,故②正确;
③命题“已知x,y∈R,若x<1或y<2,则x+y<3”的否命题是,x≥1且y≥2时,x+y≥0为真命题,则命题的逆命题也为真命题,故③正确;
④∵tanx•cosx$≥\frac{1}{2}$,即sinx$≥\frac{1}{2}$且cosx≠0,
∵x∈[0,π],∴x∈[$\frac{π}{6}$,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{5π}{6}$]
∴在区间[0,π]内,满足tanx•cosx$≥\frac{1}{2}$发生的概率为P=$\frac{\frac{5π}{6}-\frac{π}{6}}{π-0}$=$\frac{2}{3}$.故④错误,
故正确的是①②③,
故选:C
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
2.若a是$\sqrt{3}$的整数部分,b是$\sqrt{3}$的小数部分,则(a+$\frac{1}{b}$)6展开式的中间项是( )
| A. | 25+15$\sqrt{3}$ | B. | 20+3$\sqrt{15}$ | C. | 15+3$\sqrt{3}$ | D. | 22+3$\sqrt{15}$ |
17.若复数z满足(1+i)(z+1)+1-i=0,则复数$\overline z$所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.我市某苹果手机专卖店针对苹果6S手机推出无抵押分期付款购买方式,该店对最近购买苹果6S手机的100人进行统计(注:每人仅购买一部手机),统计结果如下表所示:
已知分3期付款的频率为0.15,请以此100人作为样本估计消费人群总体,并解决以下问题:
(Ⅰ)求a,b的值;
(Ⅱ)求“购买手机的3名顾客中(每人仅购买一部手机),恰好有1名顾客分4期付款”的概率;
(Ⅲ)若专卖店销售一部苹果6S手机,顾客分1期付款(即全款),其利润为1000元;分2期或3期付款,其利润为1500元;分4期或5期付款,其利润为2000元.用X表示销售一部苹果6S手机的利润,求X的分布列及数学期望.
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 35 | 25 | a | 10 | b |
(Ⅰ)求a,b的值;
(Ⅱ)求“购买手机的3名顾客中(每人仅购买一部手机),恰好有1名顾客分4期付款”的概率;
(Ⅲ)若专卖店销售一部苹果6S手机,顾客分1期付款(即全款),其利润为1000元;分2期或3期付款,其利润为1500元;分4期或5期付款,其利润为2000元.用X表示销售一部苹果6S手机的利润,求X的分布列及数学期望.
1.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是夹角为60°的两个单位向量,若$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+λ$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=2$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$,$\overrightarrow{a}⊥\overrightarrow{b}$,则λ=( )
| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | 2 |
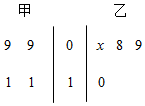 从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.
从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁. 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF=2,四边形EFCB是高为$\sqrt{3}$的等腰梯形,EF∥BC,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF=2,四边形EFCB是高为$\sqrt{3}$的等腰梯形,EF∥BC,O为EF的中点.