题目内容
12.解一元二次不等式2x2-4x+3≥0时,可先考虑以下哪个二次函数( )| A. | y=2x2-3x+4 | B. | y=2x2+3x+4 | C. | y=2x2-4x+3 | D. | y=x2+4x+3 |
分析 解一元二次不等式2x2-4x+3≥0时,可先考虑各项系数与不等式中各项系数均相等的相应的二次函数的图象和性质;
解答 解:解一元二次不等式2x2-4x+3≥0时,
可先考虑相应的二次函数y=2x2-4x+3的图象和性质,
故选:C.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
2.集合M={x|1<x+1≤3},N={x|x2-2x-3>0},则(∁RM)∩(∁RN)等于( )
| A. | (-1,3) | B. | (-1,0)∪(2,3) | C. | (-1,0]∪[2,3) | D. | [-1,0]∪(2,3] |
20.设f(x)为奇函数,且在(0,+∞)上是增函数,f(-2015)=0,则xf(x)>0的解集为( )
| A. | (-∞,2015)∪(2015,+∞) | B. | (-∞,-2015)∪(0,2015) | C. | (-2015,0)∪(0,2015) | D. | (-2015,0)∪(2015,+∞) |
4.两定点F1(-3,0),F2(3,0),P为曲线$\frac{|x|}{5}+\frac{|y|}{4}$=1上任意一点,则( )
| A. | |PF1|+|PF2|≥10 | B. | |PF1|+|PF2|≤10 | C. | |PF1|+|PF2|>10 | D. | |PF1|+|PF2|<10 |
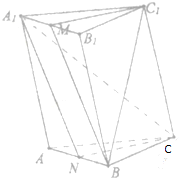 在三棱柱ABC-A1B1C1中,上下两个底面平行,侧面是平行四边形,N是AB的中点,M是A1B1的中点,求证:平面A1NC∥平面BMC1.
在三棱柱ABC-A1B1C1中,上下两个底面平行,侧面是平行四边形,N是AB的中点,M是A1B1的中点,求证:平面A1NC∥平面BMC1.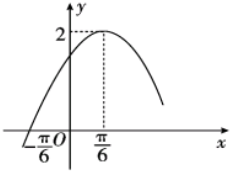 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.