题目内容
1.已知实数x、y满足$\left\{\begin{array}{l}{y≤x}\\{x+2y≤4}\\{y≥-1}\end{array}\right.$,则$\frac{y+2}{x+1}$的最小值为$\frac{1}{7}$.分析 由题意作平面区域,从而利用$\frac{y+2}{x+1}$的几何意义是点A(-1,-2)与点C(x,y)所在直线的斜率解得.
解答 解:由题意作平面区域如下,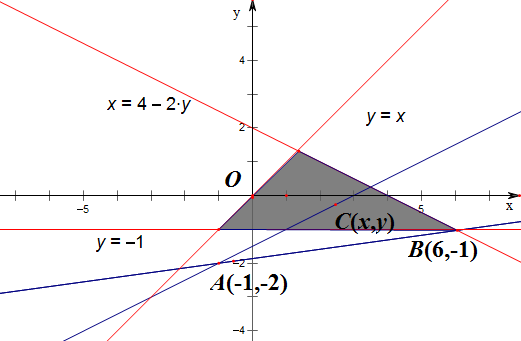
$\frac{y+2}{x+1}$的几何意义是点A(-1,-2)与点C(x,y)所在直线的斜率,
结合图象可知,
$\frac{y+2}{x+1}$的最小值为$\frac{-1+2}{6+1}$=$\frac{1}{7}$,
故答案为:$\frac{1}{7}$.
点评 本题考查了线性规划的简单应用及斜率的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知函数f(x)满足:对于任意的x1,x2∈R,都有f(x1+x2)=f(x1)+f(x2)-2015,且当x>0时,有f(x)<2015.若f(x)在[-2015,2015]上的最大值、最小值分别为M、N,则M+N的值为( )
| A. | 2014 | B. | 2015 | C. | 4028 | D. | 4030 |
12.解一元二次不等式2x2-4x+3≥0时,可先考虑以下哪个二次函数( )
| A. | y=2x2-3x+4 | B. | y=2x2+3x+4 | C. | y=2x2-4x+3 | D. | y=x2+4x+3 |
11.若logab+3logba=$\frac{13}{2}$,则用a表示b的式子是( )
| A. | b=a6 | B. | b=$\sqrt{a}$ | C. | b=a6或b=$\sqrt{a}$ | D. | b=$\root{6}{a}$且b=a2 |