题目内容

5．已知M为△ABC的边AB的中点，△ABC所在平面内有一个点P，满足$\overrightarrow{PC}=\overrightarrow{PA}+\overrightarrow{PB}$，若$|{\overrightarrow{PC}}|=λ|{\overrightarrow{PM}}|$，则λ的值为（　　）
A．2B．1C．$\frac{1}{2}$D．4

分析 由题意满足$\overrightarrow{PC}=\overrightarrow{PA}+\overrightarrow{PB}$，可得：四边形PACB是平行四边形，又M为△ABC的边AB的中点，可得PC=2PM，即可得出．

解答 解：由题意满足$\overrightarrow{PC}=\overrightarrow{PA}+\overrightarrow{PB}$，可得：四边形PACB是平行四边形，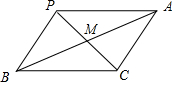
又M为△ABC的边AB的中点，
∴PC=2PM，$|{\overrightarrow{PC}}|=λ|{\overrightarrow{PM}}|$，
∴λ=2．
故选：A．

点评 本题考查了向量的平行四边形法则、平行四边形的性质，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
16．函数$f（x）=\frac{ax+b}{{{x^2}+1}}$是定义在（-∞，+∞）上的奇函数，且$f（\frac{1}{2}）=\frac{2}{5}$．
（1）求函数f（x）的解析式；
（2）判断f（x）在区间（-1，1）上的单调性，并用定义证明你的结论．
16．已知双曲线${x^2}-\frac{y^2}{3}=1$的左，右焦点分别为F1，F2，双曲线的离心率为e，若双曲线上一点P使$\frac{{sin∠P{F_2}{F_1}}}{{sin∠P{F_1}{F_2}}}=e$，则$\overrightarrow{{F_2}P}•\overrightarrow{{F_2}{F_1}}$的值为（　　）
A．3B．2C．-3D．-2
13．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，其中|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，且（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{a}$，则|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2$\sqrt{6}$．
20．已知集合$A=\{x\left|{\frac{x-3}{x+1}}\right.≤0\}，B=\{x\left|{lgx}\right.≤1\}$，则A∩B=（　　）
A．[-1，3]B．（-1，3]C．（0，1]D．（0，3]
10．已知函数f（x）=|x+t|的单调递增区间为[-1，+∞）．
（3）求不等式f（x）+1＜|2x+1|的解集M；
（4）设a，b∈M，证明：|ab+1|＞|a+b|．
16．已知数列{an}的前n项和为Sn，满足：a1=1，an+1+2Sn•Sn+1=0，则该数列的前2017项和S2017=$\frac{1}{4033}$．
12．已知平行四边形ABCD中，AB=$\sqrt{2}$，BC=3，∠ABC=45°，则$\overrightarrow{BD}$•$\overrightarrow{CD}$=5．

若实数，且，则当的最小值为时，不等式解集为_________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网