题目内容
函数f(x)=Asin(?x+φ)(A>0,?>0,|φ|<
)在区间[-
,
]上的图象如图所示.
(Ⅰ)求f(x)的解析式;
(Ⅱ)设△ABC三内角A,B,C所对边分别为a,b,c且
=
,求f(x)在(0,B]上的值域.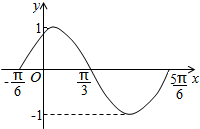
| π |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
(Ⅰ)求f(x)的解析式;
(Ⅱ)设△ABC三内角A,B,C所对边分别为a,b,c且
| cosB |
| bcosC |
| 1 |
| 2a-c |

考点:正弦函数的图象,正弦定理
专题:三角函数的求值,三角函数的图像与性质,解三角形
分析:(Ⅰ)由图可知,A=1,T=π,可求ω=2,由函数f(x)=Asin(?x+φ)过点(
,0),可得φ的值,从而可得f(x)解析式.
(Ⅱ)由已知先求B的值,又f(x)=sin(2x+
),由0<x<
,可得0≤f(x)≤1,即可求f(x)在(0,B]上的值域.
| π |
| 3 |
(Ⅱ)由已知先求B的值,又f(x)=sin(2x+
| π |
| 3 |
| π |
| 3 |
解答:
解:(Ⅰ)由图可知,A=1,T=π,则ω=2,
∵函数f(x)=Asin(?x+φ)过点(
,0)
∴φ=
∴f(x)=sin(2x+
)
(Ⅱ)由
=
,得
=
.
则cosB=
即B=
又f(x)=sin(2x+
),
由0<x<
,则0≤sin(2x+
)≤1
故0≤f(x)≤1,即值域是[0,1]
∵函数f(x)=Asin(?x+φ)过点(
| π |
| 3 |
∴φ=
| π |
| 3 |
∴f(x)=sin(2x+
| π |
| 3 |
(Ⅱ)由
| cosB |
| bcosC |
| 1 |
| 2a-c |
| cosB |
| sinBcosC |
| 1 |
| 2sinA-sinC |
则cosB=
| 1 |
| 2 |
| π |
| 3 |
又f(x)=sin(2x+
| π |
| 3 |
由0<x<
| π |
| 3 |
| π |
| 3 |
故0≤f(x)≤1,即值域是[0,1]
点评:本题主要考察了正弦函数的图象和性质,正弦定理的应用,属于基本知识的考查.

练习册系列答案
相关题目
函数y=
+
的定义域为( )
| x-1 |
| 3-x |
| A、(1,3) |
| B、[1,3] |
| C、(-∞,1)∪(3,+∞) |
| D、(1,0)∪(0,+∞) |
已知
与
为互相垂直的单位向量,
=
-2
,
=
+λ
且
与
的夹角为锐角,则实数λ的取值范围是( )
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
A、(-∞,
| ||||
B、(
| ||||
C、(-2,
| ||||
D、(-∞,-2)∪(-2,
|
按照程序框图执行,第3个输出的数是( )
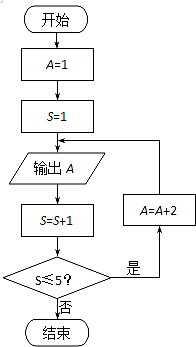

| A、4 | B、5 | C、6 | D、7 |