题目内容
如图，已知平面ABEF⊥平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠ADC=90°，AB∥CD，AD=AF=a，AB=2CD=2a．（Ⅰ）求证：AF∥平面BCE；
（Ⅱ）求证：AC⊥平面BCE；
（Ⅲ）求四棱锥C-ABEF的体积．
考点：直线与平面平行的判定,棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：（Ⅰ）求证AF∥BE，而后可得，AF∥平面BCE；（Ⅱ）由AC⊥BC，BE⊥AC可证AC⊥平面BCE；（Ⅲ）利用体积公式求四棱锥C-ABEF的体积．
解答：
解：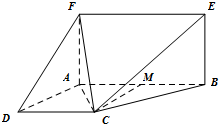
（I）因为四边形ABEF为矩形，
∴AF∥BE，BE?平面BCE，AF?平面BCE，
∴AF∥平面BCE．
（II）过C作CM⊥AB，垂足为M，∵AD⊥DC，
∴四边形ADCM为矩形．
∴AM=MB=a．
又∵AD=a，AB=2CD=2a，
∴AC=
a，BC=
a．
∴AC2+BC2=AB2，
∴AC⊥BC．
∵平面ABEF⊥平面ABCD，四边形ABEF为矩形，
∴BE⊥平面ABCD，AC?平面ABCD，
∴BE⊥AC．BE?平面BCE，BC?平面BCE，BE∩BC=B，
∴AC⊥平面BCE．
（III）∵平面ABCD⊥平面ABEF，平面ABCD∩平面ABEF=AB，
CM⊥AB，CM?平面ABCD，
∴CM⊥平面ABEF．
VC-ABEF=
CM•S矩形ABEF=
×a×a×2a=
a3．
（I）因为四边形ABEF为矩形，
∴AF∥BE，BE?平面BCE，AF?平面BCE，
∴AF∥平面BCE．
（II）过C作CM⊥AB，垂足为M，∵AD⊥DC，
∴四边形ADCM为矩形．
∴AM=MB=a．
又∵AD=a，AB=2CD=2a，
∴AC=
| 2 |
| 2 |
∴AC2+BC2=AB2，
∴AC⊥BC．
∵平面ABEF⊥平面ABCD，四边形ABEF为矩形，
∴BE⊥平面ABCD，AC?平面ABCD，
∴BE⊥AC．BE?平面BCE，BC?平面BCE，BE∩BC=B，
∴AC⊥平面BCE．
（III）∵平面ABCD⊥平面ABEF，平面ABCD∩平面ABEF=AB，
CM⊥AB，CM?平面ABCD，
∴CM⊥平面ABEF．
VC-ABEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
点评：考查了线面垂直的判定定理、线面平行的判定定理及锥体体积公式，是高考的热点，属于中档题．
练习册系列答案
相关题目
如图，四边形ABCD是矩形，BC⊥平面ABE，F是CE上一点，BF⊥平面ACE，点M，N分别是CE，DE的中点．
已知五棱锥P-ABCDE中，PA⊥平面ABCDE，五边形ABCDE中，BA⊥AE，AB⊥BC，AB=2
如图，等边△ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD=2AE，AE⊥AB．