题目内容
12.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x>0}\\{{x}^{2}+1,x≤0}\end{array}\right.$,则不等式f(x)<2的解集是(-1,1).分析 根据函数的解析式对x分类讨论,分别由指数函数的性质、一元二次不等式的解法求出对应的解集,最后再求出并集,即可得到不等式f(x)<2的解集.
解答 解:由题意知,f(x)=$\left\{\begin{array}{l}{{2}^{x},x>0}\\{{x}^{2}+1,x≤0}\end{array}\right.$,
①当x>0时,不等式f(x)<2为2x<2,
解得x<1,即0<x<1;
②当x≤0时,不等式f(x)<2为x2+1<2,
解得-1<x<1,即-1<x≤0,
综上,不等式的解集是(-1,1),
故答案为:(-1,1).
点评 本题考查一元二次不等式的解法,分段函数,以及指数函数的性质的应用,考查分类讨论思想.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
3.不等式$\frac{2-x}{x+1}$≥0的解集为( )
| A. | {x|0<x≤2} | B. | {x|-1<x≤2} | C. | {x|x>-1} | D. | R |
20.执行如图所示的程序框图,则输出的结果是( )
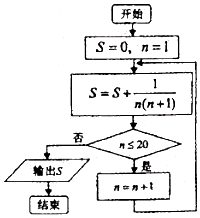

| A. | $\frac{21}{22}$ | B. | $\frac{20}{21}$ | C. | $\frac{19}{20}$ | D. | $\frac{22}{23}$ |
2.命题“若整数a,b都是偶数,则a+b是偶数”的逆否命题为( )
| A. | 若整数a,b中有一个是偶数,则a+b是偶数 | |
| B. | 若整数a,b都不是偶数,则a+b不是偶数 | |
| C. | 若整数a,b不是偶数,则a+b都不是偶数 | |
| D. | 若整数a,b不是偶数,则a+b不都是偶数 |