题目内容
8.若函数f(x)=2ax2-x-1在(0,1)内恰有一个零点,则实数a的取值范围是( )| A. | (-1,1) | B. | [1,+∞) | C. | (1,+∞) | D. | (2,+∞) |
分析 讨论a的不同取值以确定方程是否是二次方程及二次方程的根的大致位置,再由方程的根与函数的零点的关系判断即可.
解答 解:若函数f(x)=2ax2-x-1在区间(0,1)内恰有一个零点,
则方程2ax2-x-1=0在区间(0,1)内恰有一个根,
若a=0,则方程2ax2-x-1=0可化为:-x-1=0方程的解为-1,不成立;
若a<0,则方程2ax2-x-1=0不可能有正根,故不成立;
若a>0,则△=1+8a>0,且c=-1<0;
故方程有一正一负两个根,
故方程2ax2-x-1=0在区间(0,1)内恰有一个解可化为
(2a•02-0-1)(2a•12-1-1)<0;
解得,a>1;
故实数a的取值范围是(1,+∞),
故选:C.
点评 本题考查了方程的根的判断及分类讨论的数学思想应用,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.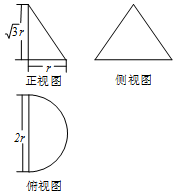 若一个空间几何体的三视图如图所示,且已知该几何体的体积为$\frac{\sqrt{3}}{6}π$,则其表面积为( )
若一个空间几何体的三视图如图所示,且已知该几何体的体积为$\frac{\sqrt{3}}{6}π$,则其表面积为( )
 若一个空间几何体的三视图如图所示,且已知该几何体的体积为$\frac{\sqrt{3}}{6}π$,则其表面积为( )
若一个空间几何体的三视图如图所示,且已知该几何体的体积为$\frac{\sqrt{3}}{6}π$,则其表面积为( )| A. | $\frac{3}{2}π+\sqrt{3}$ | B. | $\frac{3}{2}π$ | C. | $\frac{3}{4}π+2\sqrt{3}$ | D. | $\frac{3}{4}π+\sqrt{3}$ |
16.已知命题p:-x2+8x+20≥0;命题q:x2+2x+1-4m2≤0.
(1)当m∈R时,解不等式x2+2x+1-4m2≤0;
(2)当m>0时,若¬p是¬q的必要不充分条件,求实数m的取值范围.
(1)当m∈R时,解不等式x2+2x+1-4m2≤0;
(2)当m>0时,若¬p是¬q的必要不充分条件,求实数m的取值范围.
3.不等式$\frac{2-x}{x+1}$≥0的解集为( )
| A. | {x|0<x≤2} | B. | {x|-1<x≤2} | C. | {x|x>-1} | D. | R |
13.已知球的半径为4,相互垂直的两个平面分别截球面得两个圆,若两圆的公共弦长为4,则两圆的圆心距等于( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 4 |
20.执行如图所示的程序框图,则输出的结果是( )
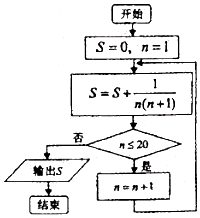

| A. | $\frac{21}{22}$ | B. | $\frac{20}{21}$ | C. | $\frac{19}{20}$ | D. | $\frac{22}{23}$ |
18.下列函数中,为奇函数又在(0,+∞)上为减函数的是( )
| A. | y=x-1 | B. | y=sinx | C. | y=($\frac{1}{2}$)x | D. | y=-|x| |
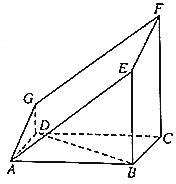 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.