题目内容
已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.
考点:圆的一般方程,圆的标准方程
专题:证明题,直线与圆
分析:选择互相垂直的两条对角线所在的直线为坐标轴.本题关键是求出圆心O′的坐标.过O′作AC的垂线,垂足为M,M是AC的中点,垂足M的横坐标与O′的横坐标一致.同理可求出O′的纵坐标.即可得出结论.
解答:
 证明:如图所示,以四边形ABCD互相垂直的对角线CA、DB所在直线分别为x轴、y轴,建立直角坐标系.设A(a,0),B(0,b),C(c,0),D(0,d).
证明:如图所示,以四边形ABCD互相垂直的对角线CA、DB所在直线分别为x轴、y轴,建立直角坐标系.设A(a,0),B(0,b),C(c,0),D(0,d).
过四边形ABCD外接圆的圆心O′分别作AC、BD、AD的垂线,垂足分别为M、N、E,则M、N、E分别是线段AC、BD、AD的中点,由线段的中点坐标公式,得
xO′=xM=
,yO′=yN=
,xE=
,yE=
.
所以|O′E|=
.
又|BC|=
,
所以|O′E|=
|BC|.
 证明:如图所示,以四边形ABCD互相垂直的对角线CA、DB所在直线分别为x轴、y轴,建立直角坐标系.设A(a,0),B(0,b),C(c,0),D(0,d).
证明:如图所示,以四边形ABCD互相垂直的对角线CA、DB所在直线分别为x轴、y轴,建立直角坐标系.设A(a,0),B(0,b),C(c,0),D(0,d).过四边形ABCD外接圆的圆心O′分别作AC、BD、AD的垂线,垂足分别为M、N、E,则M、N、E分别是线段AC、BD、AD的中点,由线段的中点坐标公式,得
xO′=xM=
| a+c |
| 2 |
| b+d |
| 2 |
| a |
| 2 |
| d |
| 2 |
所以|O′E|=
| 1 |
| 2 |
| b2+c2 |
又|BC|=
| b2+c2 |
所以|O′E|=
| 1 |
| 2 |
点评:本题考查圆的方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
古代“五行”学认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克的两种物质不相邻,则这样的排列方法有多少种(结果用数字表示).( )
| A、5 | B、10 | C、20 | D、120 |
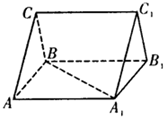
在直三棱柱ABC-A1B1C1中,若
=
,
=
,
=
,则
等于( )
| CA |
| a |
| CB |
| b |
| CC1 |
| c |
| A1B |

A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
若f(x)=
,f(f(1))=1,则a的值为.
|
| A、1 | B、2 | C、-1 | D、-2 |

