题目内容
10.已知函数f(x)=x•ex,若关于x的方程$[{f(x)+\frac{1}{2e}}]•[{f(x)-λ}]=0$有仅有3个不同的实数解,则实数λ的取值范围是[0,+∞)∪{-$\frac{1}{e}$}.分析 令f(x)=t,研究f(x)的单调性和极值,判断f(x)=t的解的情况,从而确定关于t的方程(t+$\frac{1}{2e}$)(t-λ)=0的解的分布情况,进而得出λ的范围.
解答 解:f′(x)=ex+xex=(1+x)ex,
∴当x<-1时,f′(x)<0,当x>-1时,f′(x)>0,
∴f(x)在(-∞,-1)上是减函数,在(-1,+∞)上为增函数,
∴当x=-1时,f(x)取得极小值f(-1)=-$\frac{1}{e}$.
又当x<0时,f(x)<0,f(0)=0,
作出y=f(x)的大致函数函数图象如图所示: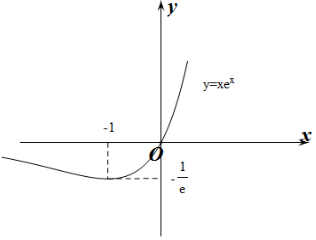
设f(x)=t,
则当t<-$\frac{1}{e}$时,方程f(x)=t无解;
当t=-$\frac{1}{e}$或t≥0时,方程f(x)=t只有一解;
当-$\frac{1}{e}$<t<0时,方程f(x)=t有两解.
∵$[{f(x)+\frac{1}{2e}}]•[{f(x)-λ}]=0$有仅有3个不同的实数解,
∴关于t的方程(t+$\frac{1}{2e}$)(t-λ)=0在(-$\frac{1}{e}$,0)和[0,+∞)∪{-$\frac{1}{e}$}上各有一解.
∵方程(t+$\frac{1}{2e}$)(t-λ)=0的解为t1=-$\frac{1}{2e}$,t2=λ.且-$\frac{1}{2e}$∈(-$\frac{1}{e}$,0),
∴λ∈[0,+∞)∪{-$\frac{1}{e}$}.
故答案为:[0,+∞)∪{-$\frac{1}{e}$}.
点评 本题考查了函数零点个数与函数单调性,极值的关系,函数单调性的判断,属于中档题.

练习册系列答案
相关题目
5.若复数z满足$z=\frac{1-i}{1+i}$(i为虚数单位),则|z|=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\sqrt{2}$ |
15.在等比数列{an}中,已知a3,a7是方程x2-6x+1=0的两根,则a5=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 3 |
19.设函数f(x)=sin(ωx+φ)(φ>0)的图象关于直线x=-1和x=2对称,则f(0)的取值集合是( )
| A. | {-1,1,-$\frac{1}{2}$} | B. | {1,-$\frac{1}{2}$,$\frac{1}{2}$} | C. | {-1,1,-$\frac{1}{2}$,$\frac{1}{2}$} | D. | {-1,1,-2,2} |
20.某十字路口的信号灯为红灯和绿灯交替出现,红灯持续的时间为60秒,小明放学回家途经该路口遇到红灯,则小明至少要等15秒才能出现绿灯的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
 椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的两顶点为A,B如图,离心率为$\frac{{\sqrt{2}}}{2}$,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.
椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的两顶点为A,B如图,离心率为$\frac{{\sqrt{2}}}{2}$,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.