题目内容
5.若复数z满足$z=\frac{1-i}{1+i}$(i为虚数单位),则|z|=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\sqrt{2}$ |
分析 利用复数代数形式的乘除运算化简,再由复数模的计算公式得答案.
解答 解:∵$z=\frac{1-i}{1+i}$=$\frac{(1-i)^{2}}{(1+i)(1-i)}=\frac{-2i}{2}=-i$,
∴|z|=1.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查复数模的求法,是基础题.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
15.在长为3m的线段AB上任取一点P,则点P与线段AB两端点的距离都大于1m的概率等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
16.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )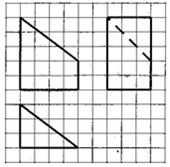

| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
17.已知实数x,y满足$\left\{\begin{array}{l}x≥0\\ y≥0\\ \frac{x}{3}+\frac{y}{4}≤1\end{array}\right.$,则$\frac{x+2y+3}{x+1}$的取值范围是( )
| A. | $[\frac{2}{3},11]$ | B. | [3,11] | C. | $[\frac{3}{2},11]$ | D. | [1,11] |
14.函数f(x)=6cos($\frac{3π}{2}$+x)-cos2x的最小值是( )
| A. | -7 | B. | -6 | C. | -5 | D. | -4 |