题目内容
10.如图1,已知四边形ABFD为直角梯形,AB∥DF,∠ADF=$\frac{π}{2}$,BC⊥DF,△AED为等边三角形,AD=$\frac{{10\sqrt{3}}}{3}$,DC=$\frac{{2\sqrt{7}}}{3}$,如图2,将△AED,△BCF分别沿AD,BC折起,使得平面AED⊥平面ABCD,平面BCF⊥平面ABCD,连接EF,DF,设G为AE上任意一点.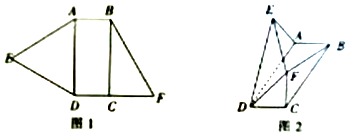
(1)证明:DG∥平面BCF;
(2)若GC=$\frac{16}{3}$,求$\frac{EG}{GA}$的值.
分析 (1)根据题意证明CD⊥平面AED,CD⊥平面BCF,得出平面AED∥平面BCF,即可证明DG∥平面BCF;
(2)根据空间中的垂直关系,利用直角三角形的边角关系,即可求出$\frac{EG}{GA}$的值.
解答 解:(1)由题意可知AD⊥DC,因为平面AED⊥平面ABCD,
平面AED∩平面ABCD=AD,
所以CD⊥平面AED,
同理CD⊥平面BCF,所以平面AED∥平面BCF;
又DG?平面AED,所以DG∥平面BCF;
(2)取AD的中点O,连接OE,则OE⊥AD,
过G作GH⊥OA,垂足为G,设GH=h;
∵∠EAD=60°,∴$AH=\frac{{\sqrt{3}}}{3}h$;
∵GC2=GH2+HD2+DC2,
∴$\frac{256}{9}={h^2}+{(\frac{{10\sqrt{3}}}{3}-\frac{{\sqrt{3}}}{3}h)^2}+\frac{28}{9}$,
化简得h2-5h+6=0,
∴h=3或h=2;
又∵$OE=\frac{{10\sqrt{3}}}{3}×\frac{{\sqrt{3}}}{2}=5$,
当h=3时,
在Rt△AOE中,$\frac{AH}{OE}=\frac{AG}{AE}=\frac{3}{5}$,
∴$\frac{EG}{GA}=\frac{2}{3}$;
当h=2时,同理可得$\frac{EG}{GA}=\frac{3}{2}$,
综上所述,$\frac{EG}{GA}$的值为$\frac{2}{3}$或$\frac{3}{2}$.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了边角关系的应用问题,是综合性题目.

练习册系列答案
相关题目
20.已知函数f(x)=ax3+bx2+cx,其导函数为f′(x)的部分值如表所示:
根据表中数据,回答下列问题:
(Ⅰ)实数c的值为6;当x=3时,f(x)取得极大值(将答案填写在横线上).
(Ⅱ)求实数a,b的值.
(Ⅲ)若f(x)在(m,m+2)上单调递减,求m的取值范围.
| x | -3 | -2 | 0 | 1 | 3 | 4 | 8 |
| f'(x) | -24 | -10 | 6 | 8 | 0 | -10 | -90 |
(Ⅰ)实数c的值为6;当x=3时,f(x)取得极大值(将答案填写在横线上).
(Ⅱ)求实数a,b的值.
(Ⅲ)若f(x)在(m,m+2)上单调递减,求m的取值范围.
5.在△ABC中,a,b,c分别为角A,B,C所对的边,若c=4,且C=60°,则ab的最大值为( )
| A. | 4 | B. | 1+$\sqrt{3}$ | C. | 16 | D. | $\frac{1+\sqrt{3}}{2}$ |
15.若全集U={x∈N|1≤x≤7},集合A={1,2,3,5},B={2,3,4},则集合CUA∩CUB等于( )
| A. | { 2,3 } | B. | { 1,5,6,7 } | C. | { 6,7 } | D. | { 1,5 } |