题目内容
12.设f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,则函数y=f(f(x))的零点之和为( )| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 求出f(x)的零点为0,1,再解方程f(x)=0和f(x)=1得出f(f(x))的所有零点.
解答 解:令f(x)=0得x=0或x=1,
∵f(f(x))=0,
∴f(x)=0或f(x)=1,
由以上过程可知f(x)=0的解为0,1,
令f(x)=1得x=-1,或x=2,
∴f(f(x))的零点之和为0+1+(-1)+2=2.
故选:C.
点评 本题考查了函数零点的计算,分段函数函数值的计算,属于中档题.

练习册系列答案
相关题目
17.已知点P(3,-4)是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$渐近线上的一点,E,F是左,右两个焦点,若$\overrightarrow{EP}•\overrightarrow{FP}=0$,则双曲线方程为( )
| A. | $\frac{x^2}{18}-\frac{y^2}{32}=1$ | B. | $\frac{x^2}{32}-\frac{y^2}{18}=1$ | C. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ |
4.已知实数x,y满足$\left\{\begin{array}{l}{|x-y|≤1}\\{|x+y|≤3}\end{array}\right.$,则|3x+y|的最大值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
1.下列函数中满足在(-∞,0)上单调递减的偶函数是( )
| A. | $y={({\frac{1}{2}})^{|x|}}$ | B. | y=|log2(-x)| | C. | $y={x^{\frac{2}{3}}}$ | D. | y=sin|x| |
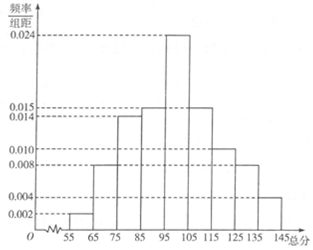 某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示.
某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示.