题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x}-1,x≤0}\\{2{x}^{2}-lnx,x>0}\end{array}\right.$,若函数y=f(x)-a恰有一个零点,则a的取值范围是[0,$\frac{1}{2}$-ln$\frac{1}{2}$).分析 判断f(x)的单调性,作出f(x)的函数图象,根据函数图象得出a的范围.
解答 解:当x>0时,f′(x)=4x-$\frac{1}{x}$=$\frac{4{x}^{2}-1}{x}$,
∴当0$<x<\frac{1}{2}$时,f′(x)<0,当x$>\frac{1}{2}$时,f′(x)>0,
∴f(x)在(0,$\frac{1}{2}$)上单调递减,在($\frac{1}{2}$,+∞)上单调递增,
∴当x=$\frac{1}{2}$时,f(x)取得极小值f($\frac{1}{2}$)=$\frac{1}{2}$-ln$\frac{1}{2}$,
作出f(x)的函数图象,如图所示: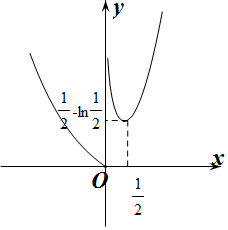
∵函数y=f(x)-a恰有一个零点,
∴0≤a<$\frac{1}{2}-$ln$\frac{1}{2}$.
故答案为:[0,$\frac{1}{2}-$ln$\frac{1}{2}$).
点评 本题考查了函数零点与函数图象的关系,函数单调性的判断与极值计算,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
12.设f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,则函数y=f(f(x))的零点之和为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
13.某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于70为合格品,小于70为次品.现随机抽取这种芯片共120件进行检测,检测结果统计如表:
已知生产一件芯片,若是合格品可盈利400元,若是次品则亏损50元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产3件芯片所获得的利润不少于700元的概率.
(Ⅱ)记ξ为生产4件芯片所得的总利润,求随机变量ξ的分布列和数学期望.
| 测试指标 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 芯片数量(件) | 8 | 22 | 45 | 37 | 8 |
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产3件芯片所获得的利润不少于700元的概率.
(Ⅱ)记ξ为生产4件芯片所得的总利润,求随机变量ξ的分布列和数学期望.
10.不等式x2-x+m>0在R上恒成立的一个必要不充分条件是( )
| A. | m>0 | B. | 0<m<1 | C. | m>$\frac{1}{4}$ | D. | m>1 |
13.已知条件p:|x+1|>2,条件q:5x-6>x2,则﹁q是﹁p的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1、BC的中点,则异面直线AB1与EF所成角的大小为 ( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
17.已知α,β∈R,则“α>β”是“α-β>sinα-sinβ”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
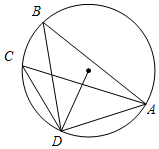 如图,圆内接四边形ABCD中,AD=DC=2BC=2,AB=3.
如图,圆内接四边形ABCD中,AD=DC=2BC=2,AB=3.