题目内容
设等差数列{an}的前n项和为Sn,已知(a2012-1)3+2014a2012=0,(a3-1)3+2014a3=4028,则下列结论正确的是( )
| A、S2014=2014,a2012<a3 |
| B、S2014=2014,a2012>a3 |
| C、S2014=2013,a2012<a3 |
| D、S2014=2013,a2012>a3 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:构造函数f(x)=(x-1)3+2014x,由函数的单调性可判a2012<a3,已知两式相加分解因式,由g(t)为增函数,且g(2)=4028,可得t=2,进而由等差数列的性质和求和公式可得.
解答:
解:构造函数f(x)=(x-1)3+2014x,
则f′(x)=3(x-1)2+2014>0,
∴函数f(x)=(x-1)3+2014x单调递增,
∵f(a3)=4028>f(a2012)=0,
∴a2012<a3,排除B和D,
已知两式相加可得(a2012-1)3+2014a2012+(a3-1)3+2014a3=4028
分解因式可得(a3+a2012-2)[(a2012-1)2-(a2012-1)(a3-1)+(a3-1)2]+2014(a3+a2012)=4028,
令a3+a2012=t,则有g(t)=[(a2012-1)2-(a2012-1)(a3-1)+(a3-1)2](t-2)+2014t,
∵[(a2012-1)2-(a2012-1)(a3-1)+(a3-1)2]>0,∴g(t)为增函数,
又∵g(2)=4028,∴必有t=2,即a3+a2012=2,
∴S2014=
=
=2014
故选:A
则f′(x)=3(x-1)2+2014>0,
∴函数f(x)=(x-1)3+2014x单调递增,
∵f(a3)=4028>f(a2012)=0,
∴a2012<a3,排除B和D,
已知两式相加可得(a2012-1)3+2014a2012+(a3-1)3+2014a3=4028
分解因式可得(a3+a2012-2)[(a2012-1)2-(a2012-1)(a3-1)+(a3-1)2]+2014(a3+a2012)=4028,
令a3+a2012=t,则有g(t)=[(a2012-1)2-(a2012-1)(a3-1)+(a3-1)2](t-2)+2014t,
∵[(a2012-1)2-(a2012-1)(a3-1)+(a3-1)2]>0,∴g(t)为增函数,
又∵g(2)=4028,∴必有t=2,即a3+a2012=2,
∴S2014=
| 2014(a1+a2014) |
| 2 |
| 2014(a3+a2012) |
| 2 |
故选:A
点评:本题考查等差数列的求和公式,涉及函数的单调性的应用和构造函数的技巧,属中档题.

练习册系列答案
相关题目
同时投掷两个骰子,则向上的点数之差的绝对值为4的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
曲线f(x)=2x在x=0处的切线方程为( )
| A、y=x-1 |
| B、y=x+1 |
| C、y=(x-1)ln2 |
| D、y=xln2+1 |
若一元二次不等式f(x)>0的解集为{x|-2<x<1},则f(2x)>0的解集为( )
| A、{x|x<-2或x>0} |
| B、{x|x<0或x>2} |
| C、{x|x>0} |
| D、{x|x<0} |
某程序框图如图所示,当程序运行后,输出T的值是( )


| A、204 | B、140 |
| C、91 | D、55 |

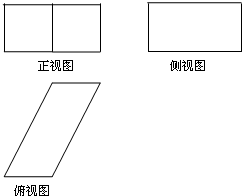 一个几何体的三视图如图所示.已知正视图为两个边长为1的正方形拼成的矩形,侧视图是一个长为
一个几何体的三视图如图所示.已知正视图为两个边长为1的正方形拼成的矩形,侧视图是一个长为