题目内容
已知关于正整数n的二次式y=n2+an(a为实数),若当且仅当n=5时,函数y有最小值,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:先将函数配方,得到不等式-
<
<-
,解出a的范围即可.
| 11 |
| 2 |
| a |
| 2 |
| 9 |
| 2 |
解答:
解:y=n2+an=(n+
)2-
,
因为n为正整数
所以-
<
<-
(当且仅当,所以不能等于)
解得:-11<a<-9.
| a |
| 2 |
| a2 |
| 4 |
因为n为正整数
所以-
| 11 |
| 2 |
| a |
| 2 |
| 9 |
| 2 |
解得:-11<a<-9.
点评:本题考查了二次函数的性质,考查了函数是最值问题,本题属于基础题.

练习册系列答案
相关题目
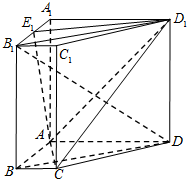 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=