曲线y=4x-x3.在点处的切线方程是( )A．y=7x+4B．y=x-4C．y=7x+2D．y=x-2 题目和参考答案——青夏教育精英家教网——

题目内容

2．曲线y=4x-x³，在点（-1，-3）处的切线方程是（　　）

A．

y=7x+4

B．

y=x-4

C．

y=7x+2

D．

y=x-2

分析求出函数的导数，求出切线的斜率，然后求解切线方程．

解答解：曲线y=4x-x³，可得y′=4-3x²，在点（-1，-3）处的切线的斜率为：4-3=1，
所求的切线方程为：y+3=x+1，
即y=x-2．
故选：D．

点评本题考查切线方程的求法，是基础题．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

12．设函数y=f（x）的图象与y=2^x+a的图象关于直线y=x对称，且f（2）+f（4）=-1，则a=（　　）

13．已知P是椭圆$\frac{{x}^{2}}{4}$+y²=1上的动点，则P点到直线l：x+y-2$\sqrt{5}$=0的距离的最小值为（　　）

$\frac{\sqrt{10}}{2}$

$\frac{\sqrt{5}}{2}$

$\frac{\sqrt{10}}{5}$

$\frac{\sqrt{2}}{5}$

10．已知命题p：?x₀∈R，x₀-2＞1gx₀；命题q：?x∈R，x²+x+1＞0，给出下列结论（　　）
①命题“p∧q”是真命题；
②命题“p∧（￢q）”是假命题；
③命题“（￢p）∨q”是真命题；
④命题“p∨（￢q）”是假命题．

17．已知$cos（\frac{π}{6}-x）=-\frac{{\sqrt{3}}}{3}$，则$cos（\frac{5π}{6}+x）+sin（\frac{2π}{3}-x）$=（　　）

7．已知函数f（x）=log（2-x）+1（m＞0，且m≠1）的图象恒过点P，且点P在直线ax+by=1，a，b∈R上，那么ab的最大值为$\frac{1}{4}$．

14．已知数列{a_n}满足${a_1}+{a_3}=\frac{5}{8}，{a_{n+1}}=2{a_n}$，其前n项和为S_n，则S_n-2a_n的值为-$\frac{1}{8}$．

11．若cos θ=-$\frac{3}{5}$，且180°＜θ＜270°，则tan $\frac{θ}{2}$的值为（　　）

±$\frac{1}{2}$

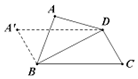如图，矩形ABCD中，AB=1，BC=$\sqrt{3}$，将△ABD沿对角线BD向上翻折，若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$，$\frac{\sqrt{13}}{2}$]内变化，则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$．