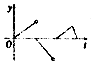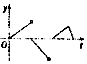题目内容
14.已知数列{an}满足${a_1}+{a_3}=\frac{5}{8},{a_{n+1}}=2{a_n}$,其前n项和为Sn,则Sn-2an的值为-$\frac{1}{8}$.分析 由题意可知{an}是等比数列,公比为2,求出a1即可得出an,Sn,从而得出Sn-2an的值.
解答 解:∵an+1=2an,∴{an}是以2为公比的等比数列,
∵a1+a3=$\frac{5}{8}$,∴a1+4a1=$\frac{5}{8}$,
解得a1=$\frac{1}{8}$,
∴an=$\frac{1}{8}×{2}^{n-1}$=2n-4,Sn=$\frac{\frac{1}{8}(1-{2}^{n})}{1-2}$=2n-3-$\frac{1}{8}$,
∴Sn-2an=2n-3-$\frac{1}{8}$-2n-3=-$\frac{1}{8}$.
故答案为:$-\frac{1}{8}$
点评 本题考查了等比数列的判断,等比数列的通项公式和求和公式,属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
4.设向量$\overrightarrow{a}$=(2,3m+2),$\overrightarrow{b}$=(m,-1).若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数m等于( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
5.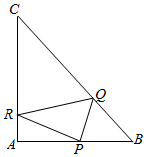 在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
 在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )| A. | 2 | B. | 1 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
2.曲线y=4x-x3,在点(-1,-3)处的切线方程是( )
| A. | y=7x+4 | B. | y=x-4 | C. | y=7x+2 | D. | y=x-2 |
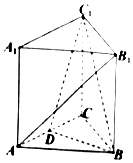 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点.
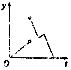
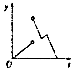
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点. 如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( )
如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( )