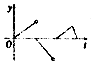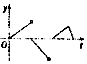题目内容
12.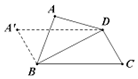 如图,矩形ABCD中,AB=1,BC=$\sqrt{3}$,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{13}}{2}$]内变化,则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$.
如图,矩形ABCD中,AB=1,BC=$\sqrt{3}$,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{13}}{2}$]内变化,则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$.
分析 过A作BD的垂线AE,则A点轨迹是以E为圆心的圆弧,以E为原点建立坐标系,设二面角A-BD-A′的大小为θ,用θ表示出A和C的坐标,利用距离公式计算θ的范围,从而确定圆弧对应圆心角的大小,进而计算出圆弧长.
解答 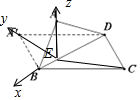 解:过A作AE⊥BD,垂足为E,连接CE,A′E.
解:过A作AE⊥BD,垂足为E,连接CE,A′E.
∵矩形ABCD中,AB=1,BC=$\sqrt{3}$,
∴AE=$\frac{\sqrt{3}}{2}$,CE=$\frac{\sqrt{7}}{2}$.
∴A点的轨迹为以E为圆心,以$\frac{\sqrt{3}}{2}$为半径的圆弧.
∠A′EA为二面角A-BD-A′的平面角.
以E为原点,以EB,EA′,EA为坐标轴建立空间直角坐标系E-xyz,
设∠A′EA=θ,则A(0,$\frac{\sqrt{3}}{2}$cosθ,$\frac{\sqrt{3}}{2}$sinθ),C(-1,-$\frac{\sqrt{3}}{2}$,0)
∴AC=$\sqrt{1+\frac{3}{4}(cosθ+1)^{2}+\frac{3}{4}si{n}^{2}θ}$=$\sqrt{\frac{5+3cosθ}{2}}$,
∴$\frac{\sqrt{10}}{2}≤$$\sqrt{\frac{5+3cosθ}{2}}$$≤\frac{\sqrt{13}}{2}$,
解得0≤cosθ≤$\frac{1}{2}$,
∴60°≤θ≤90°,
∴A点轨迹的圆心角为30°,
∴A点轨迹的长度为$\frac{π}{6}•\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}π}{12}$.
故答案为:$\frac{{\sqrt{3}}}{12}π$
点评 本题考查了空间距离的计算,建立坐标系用θ表示出AC的长是解题的关键,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | y=7x+4 | B. | y=x-4 | C. | y=7x+2 | D. | y=x-2 |
| A. | $a<\frac{2}{3}$ | B. | a>0 | C. | $0<a<\frac{2}{3}$ | D. | a<0或$a>\frac{2}{3}$ |
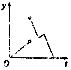
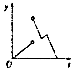
 如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( )
如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( )