题目内容
9.已知向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=1,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{7}$.分析 根据条件进行数量积的计算便可得出$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{2}$,从而便可求出$(\overrightarrow{a}+2\overrightarrow{b})^{2}=7$,这样即可求出$|\overrightarrow{a}+2\overrightarrow{b}|$的值.
解答 解:根据条件,$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{2}$;
∴$(\overrightarrow{a}+2\overrightarrow{b})^{2}={\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}=1+2+4=7$;
∴$|\overrightarrow{a}+2\overrightarrow{b}|=\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 考查向量数量积的运算及其计算公式,掌握要求$|\overrightarrow{a}+2\overrightarrow{b}|$而去求$(\overrightarrow{a}+2\overrightarrow{b})^{2}$的方法.

练习册系列答案
相关题目
2.若三个连续正整数的和是27,则在它前面的三个连续正整数的积是( )
| A. | 120 | B. | 720 | C. | 72 | D. | 210 |
14.如图,椭圆$\frac{{x}^{2}}{3}$+y2=1的左、右焦点分别为F1,F2,短轴端点分别为B1,B2,现沿B1B2将椭圆折成120°角(图二),则异面直线F1B2与B1F2所成角的余弦值为( )
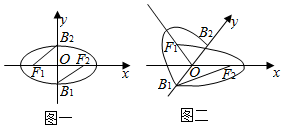

| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{1}{3}$ |
1.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | $y=\frac{1}{x}$ | B. | y=lgx | C. | y=|x|-1 | D. | $y={({\frac{1}{2}})^{lnx}}$ |
18.集合M={x|lg(1-x)<0},集合N={x|-1≤x≤1},则M∩N=( )
| A. | (0,1) | B. | [0,1) | C. | [-1,1] | D. | [-1,1) |