题目内容
6.若复数z=a+2i(i为虚数单位,a∈R)满足|z|=3,则a的值为±$\sqrt{5}$.分析 根据复数的运算性质得到a2+4=9,解出即可.
解答 解:若复数z=a+2i(i为虚数单位,a∈R)满足|z|=3,
即a2+4=9,解得:a=±$\sqrt{5}$,
故答案为:±$\sqrt{5}$.
点评 本题考查了复数求模问题,是一道基础题.

练习册系列答案
相关题目
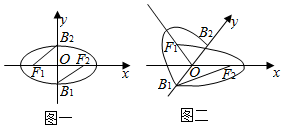
14.如图,椭圆$\frac{{x}^{2}}{3}$+y2=1的左、右焦点分别为F1,F2,短轴端点分别为B1,B2,现沿B1B2将椭圆折成120°角(图二),则异面直线F1B2与B1F2所成角的余弦值为( )

| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{1}{3}$ |
1.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | $y=\frac{1}{x}$ | B. | y=lgx | C. | y=|x|-1 | D. | $y={({\frac{1}{2}})^{lnx}}$ |
11.已知$tan(x+\frac{π}{4})=2$,则sin2x=( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
18.集合M={x|lg(1-x)<0},集合N={x|-1≤x≤1},则M∩N=( )
| A. | (0,1) | B. | [0,1) | C. | [-1,1] | D. | [-1,1) |
15.设$\frac{a-2i}{5+bi}$=1(a,b∈R,i为虚数单位),则|a+bi|的值为( )
| A. | 2$\sqrt{7}$ | B. | $\sqrt{29}$ | C. | 3$\sqrt{3}$ | D. | 5 |
16.给出定义:设f′(x)是函数y=f(x)的导函数,f″(x)是函数f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.已知函数f(x)=3x+4sinx-cosx的拐点是M(x0,f(x0)),则点M( )
| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |