题目内容
5．已知$\frac{m}{1+i}$=1-ni，其中，m，n是实数，i是虚数单位，则m-n=（ ）| A． | 3 | B． | 2 | C． | 1 | D． | -1 |
分析 已知等式整理后，利用复数相等的条件求出m与n的值，即可求出m-n的值．
解答 解：由$\frac{m}{1+i}$=1-ni，整理得：m=（1-ni）（1+i）=1+n+（1-n）i，
∴$\left\{\begin{array}{l}{m=n+1}\\{1-n=0}\end{array}\right.$，
解得：m=2，n=1，
则m-n=2-1=1，
故选：C．
点评 此题考查了复数相等的充要条件，弄清复数相等的充要条件是解本题的关键．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
2．若三个连续正整数的和是27，则在它前面的三个连续正整数的积是（ ）
| A． | 120 | B． | 720 | C． | 72 | D． | 210 |
14．如图，椭圆$\frac{{x}^{2}}{3}$+y2=1的左、右焦点分别为F1，F2，短轴端点分别为B1，B2，现沿B1B2将椭圆折成120°角（图二），则异面直线F1B2与B1F2所成角的余弦值为（ ）
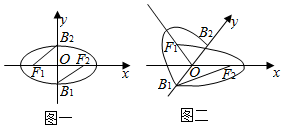
| A． | 0 | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | -$\frac{1}{3}$ |
15．设$\frac{a-2i}{5+bi}$=1（a，b∈R，i为虚数单位），则|a+bi|的值为（ ）
| A． | 2$\sqrt{7}$ | B． | $\sqrt{29}$ | C． | 3$\sqrt{3}$ | D． | 5 |