题目内容
17.已知实数a≠0,函数f(x)=$\left\{\begin{array}{l}{2x+a,x<1}\\{-x-2a,x≥1}\end{array}\right.$,若f(1-a)=f(1+a),则以直线x=a为准线的抛物线的标准方程是y2=-6x.分析 对a分类求出满足f(1-a)=f(1+a)的a的值,得到抛物线准线,由此求得以直线x=a为准线的抛物线的标准方程.
解答 解:∵实数a≠0,函数f(x)=$\left\{\begin{array}{l}{2x+a,x<1}\\{-x-2a,x≥1}\end{array}\right.$,
①若a>0,则1-a<1,1+a>1,又f(1-a)=f(1+a),
∴2(1-a)+a=-(1+a)+2a,解得a=$\frac{3}{2}$;
②若a<0,则1-a>1,1+a<1,又f(1-a)=f(1+a),
∴2(1+a)+a=-(1-a)+2a,解得a无解;
∴a=$\frac{3}{2}$.
则以直线x=a为准线的抛物线的标准方程是y2=-6x.
故答案为:y2=-6x.
点评 本题考查分段函数的应用,考查了抛物线方程的求法,是中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
10.已知a>0,b>0,若a+b=4,则( )
| A. | a2+b2有最小值 | B. | $\sqrt{ab}$有最小值 | C. | $\frac{1}{a}+\frac{1}{b}$有最大值 | D. | $\frac{1}{{\sqrt{a}+\sqrt{b}}}$有最大值 |
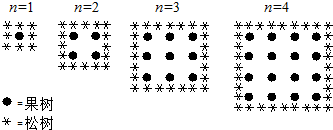 某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在如图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:
某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在如图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律: