Question

设变量x，y满足|x|+|y|≤1，求：
（1）z=x+2y的最大值；
（2）z=x²+y²-4x+4y的最小值；
（3）z=

2y+1

x-5

的最大值．

Answer 1

考点：绝对值不等式的解法

专题：不等式的解法及应用

分析：（1）化约束条件为不等式组，进而作出其对应的平面区域，变形目标函数经平移直线得最优解，代值得答案．
（2）z表示正方形及其内部的点（x，y）到（2，-2）的距离的平方减去8．求得正方形位于第四象限的边所在的直线方程为x-y-1=0，以及点（2，-2）到此直线的距离d的值，可得z=x²+y²-4x+4y的最小值．
（3）z=2•

y+ 1 2

x-5

，表示正方形及其内部的点（x，y）与点M（5，-

1

2

）连线的斜率的2倍．显然点N（0，-1）与点M（5，-

1

2

）连线的斜率最大，求得此最大值，再乘以2，即为所求．

解答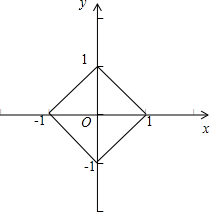： 解：（1）约束条件|x|+|y|≤1可化为：

x+y≤1，x≥0，y≥0 x-y，x≥0，y＜0 -x+y，x＜0，y≥0 -x-y，x＜0，y＜0

，
其表示的平面区域如图所示的正方形及内部：
设目标函数z=x+2y，变形可得y=-

1

2

x+

z

2

，
经平移直线可知当直线经过点（0，1）时，z=x+2y取最大值2．
（2）z=x²+y²-4x+4y=（x-2）²+（y+2）²-8，表示正方形及其内部的点（x，y）到（2，-2）的距离的平方减去8．
正方形位于第四象限的边所在的直线方程为x-y-1=0，求得点（2，-2）到此直线的距离为d=

|2+2-1|

2

=

3

2

，
可得z=x²+y²-4x+4y的最小值为

9

2

-8=-

7

2

．
（3）z=

2y+1

x-5

=2

y+ 1 2

x-5

，表示正方形及其内部的点（x，y）与点M（5，-

1

2

）连线的斜率的2倍．
显然点N（0，-1）与点M（5，-

1

2

）连线的斜率最大为

- 1 2 +1

5-0

=

1

10

，
故z=

2y+1

x-5

的最大值为2×

1

10

=

1

5

．

点评：本题考查简单线性规划，两点间的距离公式、直线的斜率公式的应用，画出满足条件的可行域，确定最优解是解决问题的关键，属中档题．