题目内容
已知a,b∈R,b≠0,曲线y=x3-ax2-bx和直线 y=ax+b有交点Q(m,n)(m,n∈Z),则a,b满足的等量关系式为 .(不能含其它参量)
考点:函数恒成立问题
专题:函数的性质及应用
分析:把交点Q(m,n)代入得:n=am+b及n=m3-am2-bm,再得出n=m3-am2-bm=m3-m(am+b)=m3-mn,从而m3=(m+1)n,验证整数可得结果.
解答:
解:∵曲线y=x3-ax2-bx和直线 y=ax+b有交点Q(m,n)(m,n∈Z),
∴把交点Q(m,n)代入得:n=am+b及n=m3-am2-bm,
n=m3-am2-bm=m3-m(am+b)=m3-mn,
∴m3=(m+1)n,
∴n=
=
=
=(m+1)2-3(m+1)+3-
∵n、(m+1)2、m+1都为整数,∴
为整数,
∴
=1或
=-1,
由
=1得m=0,进一步n=
=0,则代入n=am+b得出b=0,与已知矛盾;
由
=-1得m=-2,进一步n=
=8,则代入n=am+b得出8=-2a+b,
∴2a-b+8=0
故答案为:2a-b+8=0
∴把交点Q(m,n)代入得:n=am+b及n=m3-am2-bm,
n=m3-am2-bm=m3-m(am+b)=m3-mn,
∴m3=(m+1)n,
∴n=
| m3 |
| m+1 |
| [(m+1)-1]3 |
| m+1 |
| (m+1)3-3(m+1)2+3(m+1)-1 |
| m+1 |
| 1 |
| m+1 |
∵n、(m+1)2、m+1都为整数,∴
| 1 |
| m+1 |
∴
| 1 |
| m+1 |
| 1 |
| m+1 |
由
| 1 |
| m+1 |
| m3 |
| m+1 |
由
| 1 |
| m+1 |
| m3 |
| m+1 |
∴2a-b+8=0
故答案为:2a-b+8=0
点评:本题主要考查函数图象的交点问题,注意数学式子的恒等变形是解题的关键.

练习册系列答案
相关题目
已知空间向量
=(2,-6,c),
=(1,-3,2),若
∥
,则c=( )
| a |
| b |
| a |
| b |
| A、4 | ||
| B、0 | ||
C、
| ||
D、
|
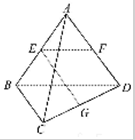 如图:已知空间四边形ABCD的边长和对角线的长都为2,点E,F,G分别是AB,AD,DC的中点求下列数量积:
如图:已知空间四边形ABCD的边长和对角线的长都为2,点E,F,G分别是AB,AD,DC的中点求下列数量积: