题目内容
17.已知函数f(x)=|2x+a|-|x-2|.(Ⅰ)当a=1时,求不等式f(x)<2的解集;
(Ⅱ)若存在实数x使f(x)≥|x-2|+3成立,求a的取值范围.
分析 (Ⅰ)将a=1代入f(x)得到:|2x+1|-|x-2|<2,通过讨论x的范围去掉绝对值号,解出不等式即可;
(Ⅱ)问题转化为|2x+a|-2|x-2|≥3成立,即|a+4|≥3成立,解出a的范围即可.
解答 解:(Ⅰ)a=1时,f(x)=|2x+1|-|x-2|<2,
x≥2时,2x+1-x+2<2,解得:x<-1,不合题意,
-$\frac{1}{2}$<x<2时,2x+1+x-2<2,解得:-$\frac{1}{2}$<x<1,
x≤-$\frac{1}{2}$时,-2x-1+x-2<2,解得:-5<x≤-$\frac{1}{2}$,
综上,不等式的解集是:{x|-5<x<1};
(Ⅱ)f(x)≥|x-2|+3成立,
即|2x+a|-2|x-2|≥3成立,
即|2x+a-2x+4|≥3成立,
即|a+4|≥3成立,
解得:a≥-1或a≤-7.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
5.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2$\sqrt{3}$,则|$\overrightarrow{a}$|=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | 3 |
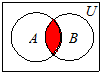
9.已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分的集合为( )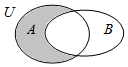

| A. | {x|-1<x<1} | B. | {x|1≤x<3} | C. | {x|x<3} | D. | {x|x≤-1} |
7.下列函数中,既是偶函数又在区间(1,2)内单调递减的是( )
| A. | f(x)=-cosx | B. | f(x)=2x+2-x | C. | f(x)=$\frac{1}{{x}^{2}}$ | D. | f(x)=$\sqrt{-x}$ |
 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=30°,PD⊥平面ABCD,AD=2,点E为AB上一点,且$\frac{AE}{AB}$=m,点F为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=30°,PD⊥平面ABCD,AD=2,点E为AB上一点,且$\frac{AE}{AB}$=m,点F为PD中点.