题目内容
19.已知函数f(x)=$\frac{1}{3}$x3-ax+1.(1)当a=1时,求f(x)在x=0处的切线方程;
(2)若f(x)在[0,1]上的最小值为$\frac{11}{12}$,求a的值.
分析 (1)求导数,确定切线的斜率,即可求f(x)在x=0处的切线方程;
(2)分类讨论,确定函数的单调性,利用f(x)在[0,1]上的最小值为$\frac{11}{12}$,即可求a的值.
解答 解:(1)当a=1时,f(x)=$\frac{1}{3}$x3-x+1,f′(x)=x2-1 …(1分)
∴f′(0)=-1 …(2分)
∵f(0)=1 …(3分)
所以切线的方程为y-1=-(x-0),即 y=-x+1 …(4分)
(2)f′(x)=x2-a …(5分)
?当a≤0时,f′(x)>0对x∈(0,1)成立,
所以f(x)在(0,1)上单调递增,f(x)在x=0处取最小值f(0)=1 …(6分)
因为1≠$\frac{11}{12}$,所以a≤0不成立 …(7分)
?当a>0时,令f'(x)=x2-a=0,x1=-$\sqrt{a}$,x2=$\sqrt{a}$,
当0<a<1时,$\sqrt{a}$<1,当x∈(0,$\sqrt{a}$)时,f'(x)<0,f(x)单调递减,x∈($\sqrt{a}$,1)时,f'(x)>0,f(x)单调递增.
所以f(x)在x=$\sqrt{a}$处取得最小值f($\sqrt{a}$)=1-$\frac{2a\sqrt{a}}{3}$=$\frac{11}{12}$,∴$a=\frac{1}{4}$.
当a≥1时,$\sqrt{a}$≥1,x∈(0,1)时,f'(x)<0,f(x)单调递减
所以f(x)在x=1处取得最小值f(1)=$\frac{4}{3}$-a.
令$\frac{4}{3}$-a=$\frac{11}{12}$,解得a=$\frac{5}{12}$(舍去)
综上$α=\frac{1}{4}$.
点评 本题考查导数知识的运用,考查分类讨论的数学思想,考查导数的几何意义、单调性,属于中档题.

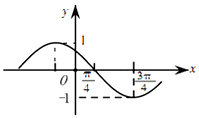
| A. | $y=sin(x+\frac{π}{4})$ | B. | $y=sin(2x+\frac{3π}{4})$ | C. | $y=cos(x+\frac{π}{4})$ | D. | $y=cos(2x+\frac{3π}{4})$ |
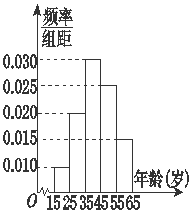 为了宣传在某市举行的“第十届中国艺术节”,筹委会举办了知识有奖问答活动,随机从15~65岁的市民中抽取n人,回答问题统计结果如图表所示:
为了宣传在某市举行的“第十届中国艺术节”,筹委会举办了知识有奖问答活动,随机从15~65岁的市民中抽取n人,回答问题统计结果如图表所示:| 组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) | a | 0.9 |
| 第3组 | [35,45) | 27 | x |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65) | 3 | 0.2 |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,筹委会决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.