题目内容
10.已知某三角函数的部分图象如图所示,则它的解析式可能是( )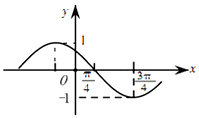
| A. | $y=sin(x+\frac{π}{4})$ | B. | $y=sin(2x+\frac{3π}{4})$ | C. | $y=cos(x+\frac{π}{4})$ | D. | $y=cos(2x+\frac{3π}{4})$ |
分析 根据已知中函数的图象,求出函数的周期进而求出|ω|=1,根据函数图象过($\frac{π}{4}$,0),利用排除法,可得答案.
解答 解:由已知中函数的周期T满足$\frac{T}{4}=\frac{3π}{4}-\frac{π}{4}$,
解得:T=2π,
故|ω|=1,故排除B,D;
当x=$\frac{π}{4}$时,$y=sin(x+\frac{π}{4})$=1≠0,故排除A,
故选:C
点评 本题考查的知识点是函数的图象,三角函数的图象和性质,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知△ABC三边长成公差为2的等差数列,且最大角的正弦值为$\frac{{\sqrt{3}}}{2}$,则这个三角形的周长是( )
| A. | 13 | B. | 15 | C. | 18 | D. | 不确定 |
5.函数f(x)=$\frac{1}{{\sqrt{x-1}}}$+(x-2)0+log2(x-1)定义域为( )
| A. | (-∞,2)∪(2,+∞) | B. | (1,+∞) | C. | (1,2)∪(2,+∞) | D. | [1,+∞) |
15.设P是平行四边形ABCD的对角线的交点,O为任一点,则$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=( )
| A. | $4\overrightarrow{OP}$ | B. | $3\overrightarrow{OP}$ | C. | $2\overrightarrow{OP}$ | D. | $\overrightarrow{OP}$ |
20.在△ABC中,角A,B,C所对边分别为a,b,c,若B=30°,b=2,c=2$\sqrt{3}$,则角C=( )
| A. | 60°或120° | B. | 60° | C. | 30°或150° | D. | 30° |