题目内容
设函数f(x)=ax-2-lnx(a∈R).
(1)若f(x)在点(e,f(e))处的切线为ex-y+2=0,求a的值;
(2)求f(x)的单调区间.
(1)若f(x)在点(e,f(e))处的切线为ex-y+2=0,求a的值;
(2)求f(x)的单调区间.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:分类讨论,导数的概念及应用,导数的综合应用
分析:(1)求出函数的导数,求得切点处的切线斜率,由已知切线方程可得a的方程,解方程即可得到a;
(2)求出导数,对a讨论,当a≤0时,当a>0时,令导数大于0,得增区间,令导数小于0,得减区间,注意定义域.
(2)求出导数,对a讨论,当a≤0时,当a>0时,令导数大于0,得增区间,令导数小于0,得减区间,注意定义域.
解答:
解:(1)函数f(x)=ax-2-lnx的导数为f′(x)=a-
,
则f(x)在点(e,f(e))处的切线斜率为k=a-
,
由切线为ex-y+2=0,可得a-
=e,
解得a=e+
;
(2)由f′(x)=a-
=
,(x>0),
当a≤0时,f′(x)<0,f(x)在x>0上递减;
当a>0时,令f′(x)>0可得x>
,
令f′(x)<0可得0<x<
.
综上可得,a≤0时,f(x)只有减区间(0,+∞);
当a>0时,f(x)的增区间为(
,+∞),减区间为(0,
).
| 1 |
| x |
则f(x)在点(e,f(e))处的切线斜率为k=a-
| 1 |
| e |
由切线为ex-y+2=0,可得a-
| 1 |
| e |
解得a=e+
| 1 |
| e |
(2)由f′(x)=a-
| 1 |
| x |
| ax-1 |
| x |
当a≤0时,f′(x)<0,f(x)在x>0上递减;
当a>0时,令f′(x)>0可得x>
| 1 |
| a |
令f′(x)<0可得0<x<
| 1 |
| a |
综上可得,a≤0时,f(x)只有减区间(0,+∞);
当a>0时,f(x)的增区间为(
| 1 |
| a |
| 1 |
| a |
点评:本题考查导数的运用:求切线斜率和单调区间,主要考查导数的几何意义和分类讨论的思想方法,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
若复数z=
(a∈R),则在复平面内,“a<4”是“z对应点在第一象限”的( )
| a+4i |
| 1+i |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知点A、B、C、D均在球O上,AB=BC=
,AC=3,若三棱锥D-ABC体积的最大值为
,则球O的表面积为( )
| 3 |
3
| ||
| 4 |
| A、36π | ||
| B、16π | ||
| C、12π | ||
D、
|
 如图,△ABC内接于⊙O,点D在OC的延长线上,AD与⊙O相切,割线DM与⊙O相交于点M,N,若∠B=30°,AC=1,则DM×DN=
如图,△ABC内接于⊙O,点D在OC的延长线上,AD与⊙O相切,割线DM与⊙O相交于点M,N,若∠B=30°,AC=1,则DM×DN= 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,∠CBD=60°,BC=2.
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,∠CBD=60°,BC=2.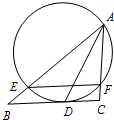 如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.
如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.