题目内容
设两个非零向量
，
，不共线，若
=
+2
，
=2
+7
，
=3（
+
），试问：A、B、C、D四点中有没有三点共线的情况？若有，是哪三点，请说明理由．
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| BC |
| e1 |
| e2 |
| CD |
| e1 |
| e2 |
考点：平面向量的基本定理及其意义,平行向量与共线向量
专题：平面向量及应用
分析：利用向量的线性运算、向量共线定理即可得出．
解答：
解：∵
=
+
=2
+7
+3（
+
）=5(
+2
)=5
，∴A，B，D三点共线．
∵不存在实数k使得
=k
，因此A，B，C三点不共线．
| BD |
| BC |
| CD |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| AB |
∵不存在实数k使得
| AB |
| BC |
点评：本题考查了向量的线性运算、向量共线定理，属于基础题．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
若复数z=
（a∈R），则在复平面内，“a＜4”是“z对应点在第一象限”的（ ）
| a+4i |
| 1+i |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
如图，在三棱锥A-BCD中，AB⊥平面BCD，BC⊥CD，∠CBD=60°，BC=2．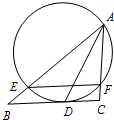
如图，过点A的圆与BC切于点D，且与AB、AC分别交于点E、F．已知AD为∠BAC的平分线，求证：EF∥BC．
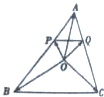如图，O是△ABC内一点，PQ∥BC，且